
【题目】已知圆O:x2+y2=3上的一动点M在x轴上的投影为N,点P满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)若直线l与圆O相切,且交曲线C于点A,B,试求|AB|的最大值.
【答案】(1)3x2+2y2=9.(2)最大值为2
【解析】
(1)设![]() 根据已知,将
根据已知,将![]() 点坐标用
点坐标用![]() 表示,代入圆
表示,代入圆![]() 方程,即可求解;
方程,即可求解;
(2)设直线l的方程为![]() ,根据条件求出
,根据条件求出![]() 关系,将直线方程与椭圆方程联立,消去
关系,将直线方程与椭圆方程联立,消去![]() ,得到关于
,得到关于![]() 的方程,利用根与系数关系,求出
的方程,利用根与系数关系,求出![]() 关于
关于![]() 的函数,利用换元法,运用函数的单调性,即可求解.
的函数,利用换元法,运用函数的单调性,即可求解.
(1)设P(x,y),M(x0,y0),则N(x0,0),∵![]() ,
,
∴(x 0﹣x,0﹣y)![]() (0,0﹣y0),即有
(0,0﹣y0),即有![]() ,
,
点M在圆O:x2+y2=3上所以x02+y02=3,
![]() 代入得
代入得![]() ,
,
∴点P的轨迹C为![]() .
.
(2)由已知可得当直线l的斜率不存在时不合题意.
故可设直线l的方程为y=kx+t,即kx﹣y+t=0.
∵圆O与直线l相切,∴圆O到直线l的距离![]() ,
,
∴t2=3(k2+1),
由![]() 可得(3+2k2)x2+4ktx+2t2﹣9=0,
可得(3+2k2)x2+4ktx+2t2﹣9=0,
![]() 恒成立.
恒成立.
设A(x1,y1),B(x2,y2),则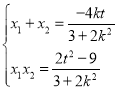 ,
,
∵t2=3(k2+1),
∴|AB|![]()
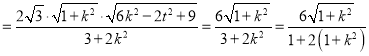 ,
,
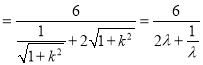 ,其中
,其中![]() .
.
令![]() ,λ∈[1,+∞).
,λ∈[1,+∞).
∵![]() 恒成立,∴g(λ)在[1,+∞)上单调递增,
恒成立,∴g(λ)在[1,+∞)上单调递增,
∴g(λ)≥g(1)=3,即![]() ,
,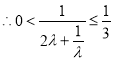 ,
,
 .
.
故|AB|的最大值为2,当且仅当λ=1,即k=0时取等号.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设点集![]() ,
,![]() 令
令![]() .从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
.从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
(1)当n=1时,求X的概率分布;
(2)对给定的正整数n(n≥3),求概率P(X≤n)(用n表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人上午的工作时间和加工的零件数,点
名工人上午的工作时间和加工的零件数,点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人下午的工作时间和加工的零件数,
名工人下午的工作时间和加工的零件数,![]() .记
.记![]() 为第
为第![]() 名工人在这一天中加工的零件总数,记
名工人在这一天中加工的零件总数,记![]() 为第
为第![]() 名工人在这一天中平均加工的零件数,则
名工人在这一天中平均加工的零件数,则![]() ,
,![]() ,
,![]() 中的最大值与
中的最大值与![]() ,
,![]() ,
,![]() 中的最大值分别是( )
中的最大值分别是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中![]() 中,已知直线l的参考方程为
中,已知直线l的参考方程为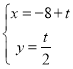 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为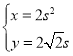 (s为参数).设P为曲线C上的动点,
(s为参数).设P为曲线C上的动点,
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)求点P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上7:00至7:15之间到某公交站搭乘公交车去上学,已知在这段时间内,共有2班公交车到达该站,到站的时间分别为7:05,7:15,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
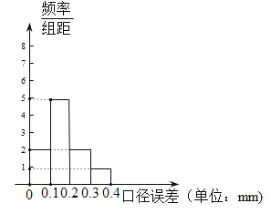

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
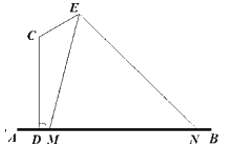
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究不同性别在处理多任务时的表现差异,召集了男女志愿者各200名,要求他们同时完成多个任务,包括解题、读地图、接电话.下图表示了志愿者完成任务所需的时间分布.以下结论,对志愿者完成任务所需的时间分布图表理解正确的是( )

①总体看女性处理多任务平均用时更短;
②所有女性处理多任务的能力都要优于男性;
③男性的时间分布更接近正态分布;
④女性处理多任务的用时为正数,男性处理多任务的用时为负数.
A.①④B.②③C.①③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com