
【题目】若f(x)=sin(2x+φ)+ ![]() cos(2x+φ)(0<φ<π)是R上的偶函数,则φ=( )
cos(2x+φ)(0<φ<π)是R上的偶函数,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵f(x)=sin(2x+φ)+ ![]() cos(2x+φ), ∴f(x)=sin(2x+φ)+
cos(2x+φ), ∴f(x)=sin(2x+φ)+ ![]() cos(2x+φ)=2cos(2x+φ﹣
cos(2x+φ)=2cos(2x+φ﹣ ![]() ),
),
∵f(x)=sin(2x+φ)+ ![]() cos(2x+φ)是偶函数,
cos(2x+φ)是偶函数,
∴φ﹣ ![]() =kπ,
=kπ,
即φ=kπ+ ![]() ,k∈Z.当k=0时,φ=
,k∈Z.当k=0时,φ= ![]()
故选:A.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】一个盒子中装有2个红球,4个白球,除颜色外,它们的形状、大小、质量等完全相同.
(1)采用不放回抽样,先后取两次,每次随机取一个球,求恰好取到1个红球,1个白球的概率;
(2)采用放回抽样,每次随机取一球,连续取5次,求恰有两次取到红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,F1 , F2分别为左右焦点,在椭圆C上满足条件
,F1 , F2分别为左右焦点,在椭圆C上满足条件 ![]() 的点A有且只有两个
的点A有且只有两个
(1)求椭圆C的方程
(2)若过点F2的两条相互垂直的直线l1与l2 , 直线l1与曲线y2=4x交于两点M、N,直线l2与椭圆C交于两点P、Q,求四边形PMQN面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD为菱形,E为棱PB的中点,O为AC与BD的交点,
(Ⅰ)证明:PD∥平面EAC
(Ⅱ)证明:平面EAC⊥平面PBD.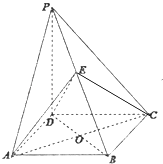
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三角形ABC的边长为2,AM是边BC上的高,沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,此时点M到平面ABC的距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正三棱柱ABC﹣A1B1C1中,点D在边BC上,AD⊥C1D. 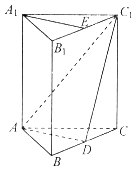
(1)求证:平面ADC1⊥平面BCC1B1;
(2)如果点E是B1C1的中点,求证:AE∥平面ADC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个样本M的数据是x1 , x2 , ,xn , 它的平均数是5,另一个样本N的数据x12 , x22 , ,xn2它的平均数是34.那么下面的结果一定正确的是( )
A.SM2=9
B.SN2=9
C.SM2=3
D.Sn2=3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC,
(1)求角B的大小;
(2)若△ABC的面积为为 ![]() 且b=
且b= ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com