
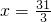 或x=13(舍去);
或x=13(舍去);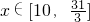 上单调递增,L(x)在
上单调递增,L(x)在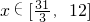 上单调递减,
上单调递减,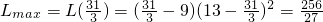 .
.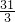 元时,该连锁分店一年的利润L最大,最大值为
元时,该连锁分店一年的利润L最大,最大值为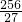 万元.
万元.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:单选题
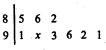 某市运动会体操比赛中,9位评委给某位参赛选手打出的分数的茎叶图如图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为90分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是
某市运动会体操比赛中,9位评委给某位参赛选手打出的分数的茎叶图如图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为90分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若统计员计算无误,则数字x应该是查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 >0的解集为
>0的解集为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com