Question

【题目】四棱锥P﹣ABCD中，PD⊥面ABCD，底面ABCD是菱形，且PD=DA=2，∠CDA=60°，过点B作直线l∥PD，Q为直线l上一动点．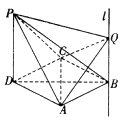
（1）求证：QP⊥AC；
（2）当二面角Q﹣AC﹣P的大小为120°时，求QB的长；
（3）在（2）的条件下，求三棱锥Q﹣ACP的体积．

Answer 1

【答案】
（1）证明：设AC∩BD=O，

∵底面ABCD是菱形，∴AC⊥BD，

∵PD⊥平ABCD，AC平面ABCD，

∴PD⊥AC，又PD平面PBD，BD平面PBD，PD∩BD=D，

∴AC⊥平面PBD，

∵BQ∥PD，∴Q∈平面PBD，

∴PQ平面PBD，

∴AC⊥PQ．

（2）解：连结OP，OQ，

∵△ACD是边长为2的等边三角形，

∴OD=OB= ，∴tan∠POD= ，

∴∠POD小于60°，

∴Q点位于B点上方，

由（1）知AC⊥平面PDBQ，

∴AC⊥OP，AC⊥OQ，

∴∠POQ为二面角P﹣AC﹣D的平面角，

在Rt△POD中， ，设QB=x，则Rt△OBQ中， ，

在直角梯形PDBQ中， ，

在△POQ中，由余弦定理得 ，故6﹣4x＞0且3x2﹣16x+5=0，

解得 ，即 ．

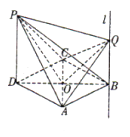
（3）解：由（2）知： ，

∴ ，

∵AC⊥面POQ，

∴ ．

【解析】（1）由AC⊥BD，AC⊥PD可得AC⊥平面PBD，故而AC⊥PQ；（2）计算∠POD的大小判断Q点大体位置，设BQ=x，计算三角形POQ的边长，利用余弦定理解出x；（3）代入公式V= 计算．