
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附: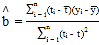 ,
,![]() . 参考数据:
. 参考数据: ![]()
科目:高中数学 来源: 题型:
【题目】如图一,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() 为侧棱
为侧棱![]() 上一点,且该四棱锥的俯视图和侧视图如图二所示.
上一点,且该四棱锥的俯视图和侧视图如图二所示.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
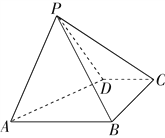
(Ⅰ)证明:AD⊥PB;
(Ⅱ)若四棱锥P-ABCD的体积等于![]() ,平面CMN∥平面PAD,且分别交PB,AB于点M,N,试确定M,N的位置,并求△CMN的面积.
,平面CMN∥平面PAD,且分别交PB,AB于点M,N,试确定M,N的位置,并求△CMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为丰富师生课余活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的
(平方米)的![]() 矩形健身场地,如图,点
矩形健身场地,如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() ,
, ![]() 米,
米, ![]() 米,
米, ![]() .设矩形
.设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正常数)
为正常数)
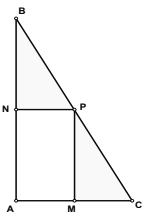
(1)试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ;
;
(3)如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价)
最低(不要求求出最低造价)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是棱
分别是棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点,点
的中点,点![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() 上移动,且
上移动,且![]() .
.
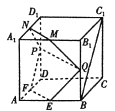
(1)当![]() 时,证明:直线
时,证明:直线![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使面
,使面![]() 与面
与面![]() 所成的二面角为直二面角?若存在,求出
所成的二面角为直二面角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最小值1,最大值9.
上有最小值1,最大值9.
(1)求实数a,b的值;
(2)设![]() ,若不等式
,若不等式![]() 在区间
在区间![]() 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)设![]() ),若函数
),若函数![]() 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列不等式的证法,再解决后面的问题:
已知![]() ,
,![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
即![]()
![]() .
.
因为对一切![]() ,恒有
,恒有![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com