
【题目】设集合![]() 是由数列
是由数列![]() 组成的集合,其中数列
组成的集合,其中数列![]() 同时满足以下三个条件:
同时满足以下三个条件:
①数列![]() 共有
共有![]() 项,
项,![]() ;②
;②![]() ;③
;③![]()
(1)若等比数列![]() ,求等比数列
,求等比数列![]() 的首项、公比和项数;
的首项、公比和项数;
(2)若等差数列![]() 是递增数列,并且
是递增数列,并且![]() ,常数
,常数![]() ,求该数列的通项公式;
,求该数列的通项公式;
(3)若数列![]() ,常数
,常数![]() ,
,![]() ,求证:
,求证:![]() .
.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
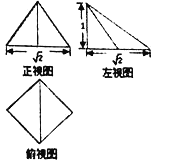
【题目】刘徽《九章算术商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
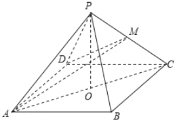
【题目】如图,在四棱锥P一ABCD中,已知![]() ,点Q为AC中点,
,点Q为AC中点,![]() 底面ABCD,
底面ABCD,![]() ,点M为PC的中点.
,点M为PC的中点.
(1)求直线PB与平面ADM所成角的正弦值;
(2)求二面角D-AM-C的正弦值;
(3)记棱PD的中点为N,若点Q在线段OP上,且![]() 平面ADM,求线段OQ的长.
平面ADM,求线段OQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
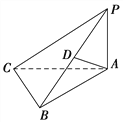
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() 且交椭圆
且交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不在
不在![]() 轴上).
轴上).
(1)若线段![]() 中点
中点![]() 的纵坐标是
的纵坐标是![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)记![]() 点关于
点关于![]() 轴的对称点为
轴的对称点为![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一幢高楼上安放了一块高约10 米的 LED 广告屏,一测量爱好者在与高楼底部同一水平线上的 C 处测得广告屏顶端A 处的仰角为 31.80°,再向大楼前进 20 米到 D 处,测得广告屏顶端 A 处的仰角为 37.38°(人的高度忽略不计).
(1)求大楼的高度(从地面到广告屏顶端)(精确到 1 米);
(2)若大楼的前方是一片公园空地,空地上可以安放一些长椅,为使坐在其中一个长椅上观看广告屏最清晰(长 椅的高度忽略不计),长椅需安置在距大楼底部 E 处多远?已知视角 ∠AMB( M 为观测者的位置, B 为广告屏 底部)越大,观看得越清晰.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com