
已知A、B为抛物线 上的不同两点,F为抛物线C的焦点,若
上的不同两点,F为抛物线C的焦点,若 则直线AB的斜率为
则直线AB的斜率为
A. B.
B. C.
C. D.
D.
D
解析试题分析:先设点A,B的坐标,求出直线方程后与抛物线方程联立消去y得到关于x的一元二次方程,求出两根,再根据向量的有关知识得到坐标的关系,进而代入抛物线的方程中得到答案解:由题意可知直线的斜存在,故可设为k(k≠0)
∵抛物线 C:y2=4x焦点F(1,0),准线x=﹣1,则直线AB的方程为y=k(x﹣1)
联立方程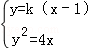 可得k2x2﹣2(2+k2)x+k2=0
可得k2x2﹣2(2+k2)x+k2=0
设A(x1,y1),B(x2,y2),则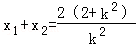 ,y1+y2=k(x1+x2﹣2)=
,y1+y2=k(x1+x2﹣2)=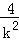 •k=
•k=
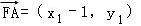 ,
,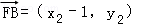
∵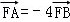 ,
,
∴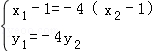 即
即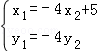 ②
②
①②联立可得,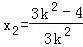 ,
,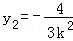
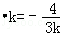 ,代入抛物线方程y2=4x可得
,代入抛物线方程y2=4x可得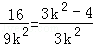 ×4,∴9k2=16∴
×4,∴9k2=16∴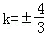 ,故选D
,故选D
考点:直线与抛物线的位置关系
点评:本题主要考查直线与抛物线的位置关系,抛物线定义的应用以及向量的有关知识


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com