Question

在-1到1之间任取两个实数，则它们的绝对值之和大于1的概率是    ．

Answer 1

【答案】分析：本题可以利用几何概率模型求解，令两个数分别是x，y∈[-1，1]，所研究事件是“|x|+|y|＞1”作出图形，由图形得出概率即可
解答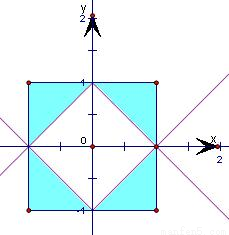：解：设两个数分别是x，y；x，y∈[-1，1]，
所研究事件是“|x|+|y|＞1”
如图总的基本事件对应的面积是4，
事件“|x|+|y|＞1”对应的面积（阴影部分）是大正方形面积的一半，
则它们的绝对值之和大于1的概率是：．
故答案为：．
点评：本题考查几何概率模型，解题的关键是能将问题转化为几何概率模型求解，本题是一个二维几何概率模型的问题，此类题一般规律是这样的，如果出现一个变量则是一维的概率模型，两个变量则建立一个二维的几何概率模型求解，如本题；三个变量的就应该用立体几何模型来研究．