
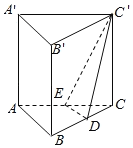
【题目】如图,在正三棱柱![]() 中,底面
中,底面![]() 边长为2,
边长为2,![]() 为
为![]() 的中点,三棱柱
的中点,三棱柱![]() 的体积.
的体积.

(1)求三棱柱的表面积;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)由三棱柱体积![]() ,求出高AA′=3,由此能求出三棱柱的表面积;(2)取AC中点E,连结DE、C′E,由D为BC中点,得DE∥AB,从而∠C′DE是异面直线AB与C′D所成角(或所成角的补角),由此能求出异面直线AB与C′D所成角的余弦值.
,求出高AA′=3,由此能求出三棱柱的表面积;(2)取AC中点E,连结DE、C′E,由D为BC中点,得DE∥AB,从而∠C′DE是异面直线AB与C′D所成角(或所成角的补角),由此能求出异面直线AB与C′D所成角的余弦值.
详解:(1)∵在正三棱柱ABC﹣A′B′C′中,底面△ABC边长为2,D为BC的中点,三棱柱体积![]() ,
,
![]()
解得高AA′=3,
∴三棱柱的表面积:![]() =
= ![]() ;
;
(2)取AC中点E,连结DE、C′E,
∵D为BC中点,∴DE∥AB,
∴∠C′DE是异面直线AB与C′D所成角(或所成角的补角),
∵DE=![]() AB=1,C′D=C′E=
AB=1,C′D=C′E=![]() =
=![]() =
=![]() ,
,
∴cos∠C′DE=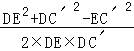 =
=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数 ![]() .
.
(1)求函数 ![]() 的最大值;
的最大值;
(2)对于任意 ![]() ,且
,且 ![]() ,是否存在实数
,是否存在实数 ![]() ,使
,使 ![]() 恒成立,若存在求出
恒成立,若存在求出 ![]() 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
(3)若正项数列 ![]() 满足
满足 ![]() ,且数列
,且数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,试判断
,试判断 ![]() 与
与 ![]() 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分.)
数列中{an},a1=8,a4=2,且满足an+2= 2an+1- an,
(1)求数列{an}的通项公式;
(2)设Sn=![]() ,求Sn
,求Sn
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,面![]() 为正方形,面
为正方形,面![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
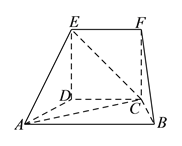
(I)求证: ![]() 平面
平面![]() .
.
(II)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com