
【题目】已知长方体ABCD﹣A1B1C1D1中,底面ABCD为正方形,DD1⊥平面ABCD,AB=4,AA1=2,点E1在棱C1D1上,且D1E1=3.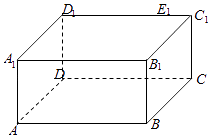
(Ⅰ)在棱CD上确定一点E,使得直线EE1∥平面D1DB,并写出证明过程;
(Ⅱ)若动点F在正方形ABCD内,且AF=2,请说明点F的轨迹,探求E1F长度的最小值并求此时直线E1F与平面ABCD所成角的正弦值.
【答案】解:(Ⅰ)连接D1B,DB,当DE=3时,直线EE1∥平面D1DB,
证明:∵DE∥D1E1,DE=D1E1,∴四边形DEE1D1为平行四边形,
∵EE1∥DD1,DD1平面D1DB,EE1平面D1DB,
∴直线EE1∥平面D1DB;
(Ⅱ)∵动点F在正方形ABCD内,且AF=2,∴点F的轨迹为以A为圆心,以2为半径的 ![]() 圆周.
圆周.
连接AE,则AE= ![]() =5,∴EF的最短距离为AE﹣AF=3,
=5,∴EF的最短距离为AE﹣AF=3,
∵E1F= ![]() ,∴E1F的长度最小值为
,∴E1F的长度最小值为 ![]() =
= ![]() .
.
∵EE1⊥平面ABCD,∴∠E1FE为线E1F与平面ABCD所成的角
∴sin∠E1FE= ![]() =
= ![]() =
= ![]() ,即直线E1F与平面ABCD所成的角的正弦值为
,即直线E1F与平面ABCD所成的角的正弦值为 ![]() .
.
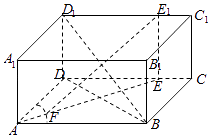
【解析】(Ⅰ)由题意可知连接D1B,DB,当DE=3时,根据线面平行的判定定理可证直线EE1∥平面D1DB。
(Ⅱ)由题意可得动点F在正方形ABCD内,且AF=2,∴点F的轨迹为以A为圆心,以2为半径的 ![]() 圆,连接AE,EF的最短距离为AE﹣AF=3,根据勾股定理可得E1F的长度最小值为
圆,连接AE,EF的最短距离为AE﹣AF=3,根据勾股定理可得E1F的长度最小值为![]() .再由线面角的定义找出∠E1FE为线E1F与平面ABCD所成的角,由
.再由线面角的定义找出∠E1FE为线E1F与平面ABCD所成的角,由![]() 可求得正弦值.
可求得正弦值.
【考点精析】认真审题,首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的(产品净重,单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,下列命题中:①样本中净重大于或等于98克并且小于102克的产品的个数是60;②样本的众数是101;③样本的中位数是 ![]() ; ④样本的平均数是101.3.
; ④样本的平均数是101.3.
正确命题的代号是(写出所有正确命题的代号).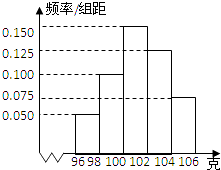
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 过点(1,e).
过点(1,e).
(1)求y=f(x)的单调区间;
(2)当x>0时,求 ![]() 的最小值;
的最小值;
(3)试判断方程f(x)﹣mx=0(m∈R且m为常数)的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com