
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的个数为( )
处取得最大值,则下列命题正确的个数为( )
①当![]() 时,m的取值范围是
时,m的取值范围是 ;②将
;②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;③函数
个单位后所对应的函数为偶函数;③函数![]() 的最小正周期为
的最小正周期为![]() ;④函数
;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=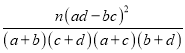 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过焦点F的直线
的焦点为F,过焦点F的直线![]() 交抛物线于A,B两点,设AB的中点为M,A,B,M在准线上的射影分别为C,D,N.
交抛物线于A,B两点,设AB的中点为M,A,B,M在准线上的射影分别为C,D,N.
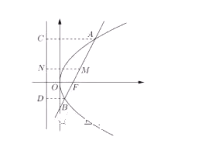
(1)求直线FN与直线AB的夹角![]() 的大小;
的大小;
(2)求证:点B,O,C三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为提高学生的身体素质,实施“每天一节体育课”,并定期对学生进行体能测验在一次体能测验中,某班甲、乙、丙三位同学的成绩(单位:分)及班内排名如表(假定成绩均为整数)现从该班测验成绩为94和95的同学中随机抽取两位,这两位同学成绩相同的概率是( )
成绩/分 | 班内排名 | |
甲 | 95 | 9 |
乙 | 94 | 11 |
丙 | 93 | 14 |
A.0.2B.0.4C.0.5D.0.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:{an}是公比大于1的等比数列,Sn为其前n项和,S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=log2a3n+1,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 定义如下:
定义如下: ![]() ,
,
(1)若![]() ,写出
,写出![]() ,
,![]() ,
,![]() ;
;
(2)求证:数列![]() 单调递增的充要条件是
单调递增的充要条件是![]() 为偶数;
为偶数;
(3)若![]() 为奇数,是否存在
为奇数,是否存在![]() 满足
满足![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,若鳖臑
,若鳖臑![]() 的外接球的体积为
的外接球的体积为![]() ,则阳马
,则阳马![]() 的外接球的表面积等于______.
的外接球的表面积等于______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为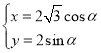 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的值;
的值;
(2)若矩形![]() 内接于曲线
内接于曲线![]() 且四边与坐标轴平行,求其周长的最大值.
且四边与坐标轴平行,求其周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,…,
,…,![]() 为1,2,…,10的一个排列,则满足对任意正整数m,n,且
为1,2,…,10的一个排列,则满足对任意正整数m,n,且![]() ,都有
,都有![]() 成立的不同排列的个数为( )
成立的不同排列的个数为( )
A.512B.256C.255D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com