
分析 分析函数f(x)=-2($\frac{{2}^{x}-1}{{2}^{x}+1}$)的定义域,单调性,值域,可得结论.
解答 解:函数f(x)=-2($\frac{{2}^{x}-1}{{2}^{x}+1}$)的定义域为R;
函数f(x)在R上为减函数,故在(0,+∞)上单调递减;
当x→+∞时,f(x)→-2,故f(x)>-2;
函数的值域为:(-2,2),故对于任意的d∈(-2,0),总存在x0,使f(x0)<d.
故满足条件的函数可以是f(x)=-2($\frac{{2}^{x}-1}{{2}^{x}+1}$),
故答案为:f(x)=-2($\frac{{2}^{x}-1}{{2}^{x}+1}$),答案不唯一
点评 本题考查的知识点是抽象函数及其应用,函数的单调性,函数的奇偶性,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}+1$ | C. | 2 | D. | $\sqrt{5}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
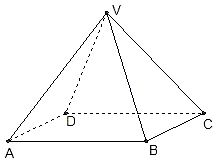 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形,试画出二面角V-AB-C的平面角,并求出它的度数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
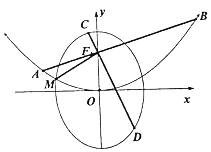 已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.
已知F1为椭圆C1:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点,F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=$\frac{5}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2] | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
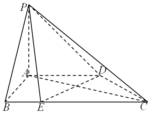 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD=$\frac{1}{2}$BC,$\overrightarrow{BE}$=$\frac{1}{4}$$\overrightarrow{BC}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14π | B. | 16π | C. | 13π | D. | 15π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com