练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．如图1是遂宁市某校高中学生身高的条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10（如A2表示身高（单位：cm）[150，155）内的学生人数）．图2是图1中身高在一定分为内学生人数的一个算法流程图．现要统计身高在160～175cm（含160cm，不含175cm）的学生人数，那么在流程图中的判断框内应填入的条件是（　　）
    A．i＜6B．i＜7C．i＜8D．i＜9

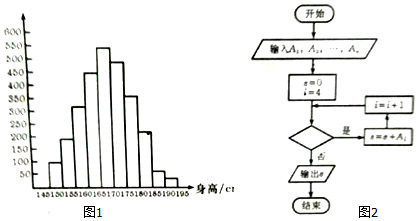
    分析 该流程图的目的是算出身高在[160，175）内的学生人数，可得循环体需计算i=4、5、6时四个Ai的和，由此可得判断框内应填写的条件是：“i＜7”．

    解答 解：为了统计身高在[160，175）内的学生人数，先算出从160到175的小组分别有
    [160，165），[165，170），[170，175）共有三组，分别为第4组、第5组、第6组．
    因此，当i=4时开始，直到i=6时算出这四组的频数之和，
    可得判断框内应填写的条件是：“i＜7”．
    故选：B．

    点评 本题以统计条形图为载体，计算身高在[160，175）内的学生人数，考查了频率直方分布图的理解和循环结构的程序框图等知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．已知直线C1：$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$（ t 为参数），曲线C2：$\left\{\begin{array}{l}{x=rcosθ}\\{y=rsinθ}\end{array}\right.$（r＞0，θ为参数）．
    （1）当r=1时，求C 1 与C2的交点坐标；
    （2）点P 为曲线 C2上一动点，当r=$\sqrt{2}$时，求点P 到直线C1距离最大时点P 的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．20160-log3（3$\frac{3}{8}$）${\;}^{-\frac{1}{3}}}$=2-log32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．为了提高学生学习数学的兴趣，某校决定在每周的同一时间开设《数学史》、《生活中的数学》、《数学与哲学》、《数学建模》四门校本选修课程，甲、乙、丙三位同学每人均在四门校本课程中随机选一门进行学习，假设三人选择课程时互不影响，且每一课程都是等可能的．
    （1）求甲、乙、丙三人选择的课程互不相同的概率；
    （2）设X为甲、乙、丙三人中选修《数学史》的人数，求X的分布列和数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知函数$f（x）=\left\{\begin{array}{l}{2^x}-1（{x≤0}）\\ f（{x-1}）+1（{x＞0}）\end{array}\right.$，把函数g（x）=f（x）-x的零点的顺序排列成一个数列，则该数列的通项公式为（　　）
    A．${a_n}=\frac{{n（{n-1}）}}{2}$B．an=n（n-1）C．an=n-1D．${a_n}={2^n}-2$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

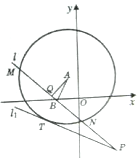    8．已知以A（-1，2）点为圆心的圆与直线${l_1}：\frac{1}{2}x+y+\frac{7}{2}=0$相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l1相交于点P．
    （1）求圆A的方程；
    （2）当$|{MN}|=2\sqrt{19}$时，求直线l的方程；
    （3）$\overrightarrow{BP}•\overrightarrow{BQ}$是否是定值，如果是，求出这个定值；如果不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

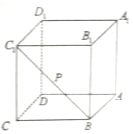    15．如图，点P是正方体ABCD-A1B1C1D1的面对角线BC1（线段BC1）上运动，给出下列五个命题：
    ①直线AD与直线B1P为异面直线；
    ②A1P∥平面ACD1；
    ③三棱锥A-D1PC的体积为定值；
    ④面PDB1⊥面ACD1；
    ⑤直线AP与平面ACD1所成角的大小不变．
    其中真命题的编号为①②③④．（写出所有真命题的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

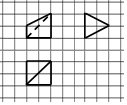    1．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（　　）
    A．8πB．$\frac{25}{2}$πC．12πD．$\frac{41}{4}$π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．点C在线段AB上，且$\frac{AC}{CB}$=$\frac{5}{2}$，$\overrightarrow{AC}$=λ$\overrightarrow{AB}$，$\overrightarrow{BC}$=μ$\overrightarrow{AB}$，则λ+μ=$\frac{3}{7}$．

    查看答案和解析>>

    同步练习册答案