
 ֱ��l��y=k��x-1������֪��Բ
ֱ��l��y=k��x-1������֪��Բ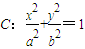 �����㣨0��
�����㣨0��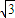 ����������Ϊ
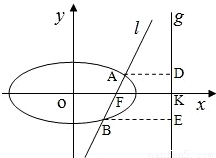
����������Ϊ ��������ԲC���ҽ���F��ֱ��l����Բ��A��B���㣬��A��F��B��ֱ��x=4�ϵ���Ӱ����Ϊ��D��K��E��
��������ԲC���ҽ���F��ֱ��l����Բ��A��B���㣬��A��F��B��ֱ��x=4�ϵ���Ӱ����Ϊ��D��K��E�� ����ֱ��l����б�DZ仯ʱ��̽���+�̵�ֵ�Ƿ�Ϊ��ֵ�����ǣ������+�̵�ֵ������˵�����ɣ�
����ֱ��l����б�DZ仯ʱ��̽���+�̵�ֵ�Ƿ�Ϊ��ֵ�����ǣ������+�̵�ֵ������˵�����ɣ�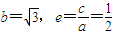 ����Ϊa2=b2+c2a2=4��c2=1���ɴ��������ԲC�ķ��̣�
����Ϊa2=b2+c2a2=4��c2=1���ɴ��������ԲC�ķ��̣� �ã�3+4k2��x2-8k2x+4k2-12=0������Τ�ﶨ��������������ܹ��Ƶ�����ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ
�ã�3+4k2��x2-8k2x+4k2-12=0������Τ�ﶨ��������������ܹ��Ƶ�����ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ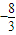 ��
��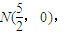 ���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ���
���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ��� ��
��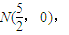 ��֤��
��֤��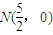 Ҳ��ֱ��lBD�ϣ����Ե�m�仯ʱ��AE��BD�ཻ�ڶ���
Ҳ��ֱ��lBD�ϣ����Ե�m�仯ʱ��AE��BD�ཻ�ڶ���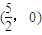 ��
��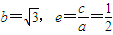 ����Ϊa2=b2+c2a2=4��c2=1������ԲC�ķ���
����Ϊa2=b2+c2a2=4��c2=1������ԲC�ķ���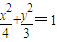 ��3�֣�
��3�֣�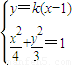 �ã�3+4k2��x2-8k2x+4k2-12=0��
�ã�3+4k2��x2-8k2x+4k2-12=0��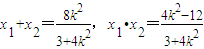 ��6�֣�
��6�֣�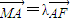 ��
�� ��ͬ����
��ͬ���� ��8�֣�
��8�֣�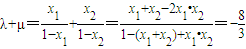
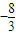 ����10�֣�
����10�֣�
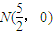 ��11�֣�
��11�֣�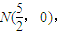 ��
��
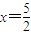 ʱ��
ʱ��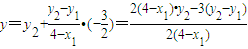 =
= =
=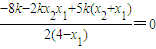 ���
���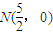 ��ֱ��lAE�ϣ�ͬ����֤����
��ֱ��lAE�ϣ�ͬ����֤����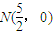 Ҳ��ֱ��lBD�ϣ��൱m�仯ʱ��AE��BD�ཻ�ڶ���
Ҳ��ֱ��lBD�ϣ��൱m�仯ʱ��AE��BD�ཻ�ڶ���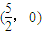



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
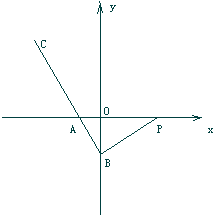 ��ͼ����ֱ֪��������PAB��ֱ�Ƕ���ΪB����P������Ϊ��3��0������B��y���ϣ���A��x��ĸ������ϣ���BA���ӳ�����ȡһ��C��ʹ
��ͼ����ֱ֪��������PAB��ֱ�Ƕ���ΪB����P������Ϊ��3��0������B��y���ϣ���A��x��ĸ������ϣ���BA���ӳ�����ȡһ��C��ʹ| BC |
| BA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 2 |
| AE |
| 3 |
| ON |
| 1 |
| 2 |
| OA |
| OF |
| 3 |
| BR |
| BS |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| OA |
| OB |
| OM |
| OA |
| OB |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com