
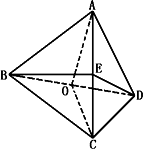
如图,四面体ABCD的棱BD长为2,其余各棱的长均是![]() ,求:二面角A-BD-C、A-BC-D、B-AC-D的大小.
,求:二面角A-BD-C、A-BC-D、B-AC-D的大小.
|
解析:(1)取BD的中点O,连AO、OC.在ΔABD中,∵AB=AD= ∴ΔABD是等腰直角三角形,AO⊥BD,同理OC⊥BD. ∴∠AOC是二面角A-BD-C的平面角 又AO=OC=1,AC= (2)∵二面角A-BD-C是直二面角,AO⊥BD,∴AO⊥平面BCD. ∴ΔABC在平面BCD内的射影是ΔBOC. ∵SΔOCB= (3)取AC的中点E,连BE、DE.∵AB=BC,AD=DC, ∴BD⊥AC,DE⊥AC,∴∠BED就是二面角的平面角. 在ΔBDE中,BE=DE= ∴二面角B-AC-D的大小是π-arccos 评析:本例提供了求二面角大小的方法:先作出二面角的平面角,再利用其所在的三角形算出角的三角函数值,或利用面积的射影公式 |


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
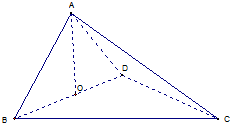 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.查看答案和解析>>
科目:高中数学 来源: 题型:
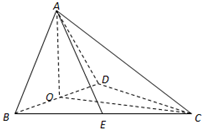 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com