
【题目】已知点P(0,-2),椭圆E: ![]() 的离心率为
的离心率为![]() ,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由直线PF的斜率和离心率列方程组求解即可;
(2)当直线l与y轴平行时,易得△AOB面积为![]() ,当直线l与y轴不平行时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),由直线与椭圆联立得(2k2+1)x2+4kmx+2(m2-1)=0,用弦长公式和点到直线距离公式求解面积即可.
,当直线l与y轴不平行时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),由直线与椭圆联立得(2k2+1)x2+4kmx+2(m2-1)=0,用弦长公式和点到直线距离公式求解面积即可.
试题解析:
(1)设F(c,0),由已知得,直线PF的斜率k=![]() ,得c=1,又
,得c=1,又![]() ,
,
则![]() ,b=1,故椭圆E的方程为
,b=1,故椭圆E的方程为![]()
(2)记点O到直线l的距离为d,则![]() ,
,
①当直线l与y轴平行时,直线l的方程为![]() ,易求
,易求![]() ,∴
,∴![]() ,
,
②当直线l与y轴不平行时,设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2),
由已知得![]() ,∴
,∴![]() ,
,
由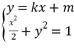 得(2k2+1)x2+4kmx+2(m2-1)=0,又△=10k2+2>0,
得(2k2+1)x2+4kmx+2(m2-1)=0,又△=10k2+2>0,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
![]() ,
,
![]() ,当且仅当k=±1时取等号,
,当且仅当k=±1时取等号,
综上当k=±1时,△AOB面积的最大值为![]()


科目:高中数学 来源: 题型:
【题目】如图,点列{An}、{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+1 , n∈N* , |BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+1 , n∈N* , (P≠Q表示点P与Q不重合)若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )
A.{Sn}是等差数列
B.{Sn2}是等差数列
C.{dn}是等差数列
D.{dn2}是等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P﹣ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.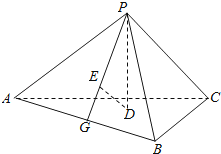
(1)证明:G是AB的中点;
(2)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x+1|﹣|2x﹣3|.
(1)在图中画出y=f(x)的图象;
(2)求不等式|f(x)|>1的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}中,a3+a4=4,a5+a7=6.
(1)求{an}的通项公式;
(2)设bn=[an],求数列{bn}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a-![]() -lnx,g(x)=ex-ex+1.
-lnx,g(x)=ex-ex+1.
(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;
(2)若f(x)=0恰有一个解,求a的值;
(3)若g(x)≥f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是椭圆C: ![]() =1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:

将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的22列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com