
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 有两个相异零点
有两个相异零点![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)对f′(x)![]() 中的k分类讨论,根据f′(x)的正负判断函数
中的k分类讨论,根据f′(x)的正负判断函数![]() 的单调性即可.
的单调性即可.
(2)由题意得lnx1﹣kx1=0,lnx2﹣kx2=0,两式作差可得,lnx1﹣lnx2=k(x1﹣x2),k=![]() ,要证lnx1+lnx2>2即k(x1+x2)>2,将k代换后,化简变形得
,要证lnx1+lnx2>2即k(x1+x2)>2,将k代换后,化简变形得![]() ,设t
,设t![]() 1,构造函数g(t),利用新函数的导数求出单调区间,证得g(t)>g(1)=0即可.
1,构造函数g(t),利用新函数的导数求出单调区间,证得g(t)>g(1)=0即可.
(1)![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(2)因为![]() ,
,![]() 是
是![]() 的两个零点,则
的两个零点,则![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
要证![]() ,只要证
,只要证![]() ,即证
,即证![]() ,
,
即证![]() ,即证
,即证![]() ,只要证
,只要证![]() .
.
设![]() ,则只要证
,则只要证![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是一种反映和评价空气质量的方法,
是一种反映和评价空气质量的方法,![]() 指数与空气质量对应如下表所示:
指数与空气质量对应如下表所示:

如图是某城市2018年12月全月的指![]() 数变化统计图.
数变化统计图.

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半月的空气质量
C. 从![]() 数据看,前半月的方差大于后半月的方差
数据看,前半月的方差大于后半月的方差
D. 从![]() 数据看,前半月的平均值小于后半月的平均值
数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 等于( )
等于( )
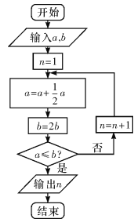
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形
为平行四边形
∠ADC=45°,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p是r的充分条件而不是必要条件,q是r的充分条件,s是r的必要条件,q是s的必要条件。现有下列命题:①s是q的充要条件;②p是q的充分条件而不是必要条件;③r是q的必要条件而不是充分条件;④![]() 是
是![]() 的必要条件而不是充分条件;⑤r是s的充分条件而不是必要条件.则正确命题序号是_______.
的必要条件而不是充分条件;⑤r是s的充分条件而不是必要条件.则正确命题序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com