解:函数f(x)的定义域为R
f′(x)=(2ax-2)e
-x-(ax
2-2x)e
-x=[-ax
2+2(a+1)x-2]e
-x,
(I)当a=0时,f′(x)=(2x-2)e
-x,
由f′(x)<0,得x<1,f′(x)>0得x>1
∴x=1是函数f(x)的极小值点
当a>0时,令f′(x)=0得-ax
2+2(a+1)x-2=0
解得该方程的两个实根为
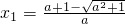
,
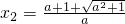
,显然x
1<x
2,
随着x的变化,f′(x)、f(x)的变化请况如下表

∴
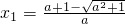
是函数的极小值点,
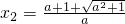
是函数的极大值点
(2)f'(x)=[-ax
2+2(a+1)x-2]e
-x,
令g(x)=ax
2-2(a+1)x+2
①若a=0,则g(x)=-2x+2,在(-1,1)内,g(x)≥0,
即f'(x)≤0,函数f(x)在区间[-1,1]上单调递减.
②若a>0,则g(x)=ax
2-2(a+1)x+2,其图象是开口向上的抛物线,对称轴为x=

>1,
∵g(1)=-a<0,g(-1)=3a+4>0,即在(-1,1)内g(x)先正后负,f′(x)先负后正,
函数f(x)在区间[-1,1]上不可能单调
③若a<0,则g(x)=ax
2-2(a+1)x+2,其图象是开口向下的抛物线,
当且仅当g(-1)≥0且g(1)≥0,即-

≤a<0时,在(-1,1)内g(x)>0,f'(x)<0,
函数f(x)在区间[-1,1]上单调递减.
综上所述,函数f(x)在区间[-1,1]上单调递减时,a的取值范围是-

≤a≤0.
(3)由(1)知,当a=0时,f(x)=(-2x)e
-x,在x=1处取得最小值
∴对?x∈R,(-2x)e
-x≥f(1)=-2e
-1,即xe
-x,≤e
-1,e
x≥ex
令x=n,则e
n≥en,即e≥e,e
2≥2e,e
3≥3e…,e
n≥en
将上述不等式左右分别相乘得:e
1+2+3+…+n=n!e
n,
即

分析:(1)先确定函数的定义域然后求出函数的导涵数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间,然后根据极值的定义判定极值即可.
(2)令导函数f′(x)=[-ax
2+2(a+1)x-2]•e
-x≤0在x∈[-1,1]时恒成立即可求出a的范围.
(3)利用(1)中的结论,构造一个函数不等式,进而转化为数列不等式,利用全正同向不等式相乘,不等号方向不变性即可证得结论
点评:本题主要考查了利用导数研究函数的极值,以及函数单调区间等有关基础知识,不等式恒成立问题的解法,函数与数列的综合运用,考查运算求解能力,转化化归能力,分类讨论能力,难度较大.

 ,这里n!=1×2×…×n.
,这里n!=1×2×…×n.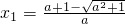 ,
,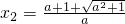 ,显然x1<x2,
,显然x1<x2,
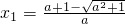 是函数的极小值点,
是函数的极小值点,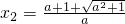 是函数的极大值点
是函数的极大值点 >1,
>1, ≤a<0时,在(-1,1)内g(x)>0,f'(x)<0,
≤a<0时,在(-1,1)内g(x)>0,f'(x)<0, ≤a≤0.
≤a≤0.


 ,这里n!=1×2×…×n.
,这里n!=1×2×…×n.