
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
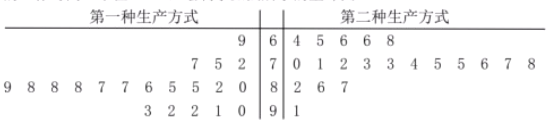
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表,再根据列联表,能否有99.9%的把握认为两种生产方式的效率有差异?
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
附: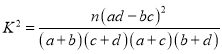 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)第二种生产方式的效率更高,理由见解析,(2)中位数为79,列联表见解析,有99.9%的把握认为两种生产方式的效率有差异
【解析】
(1)观察茎叶图数据,可从均值,中位数,分布的对称性多个角度说明即可(2)求出中位数,列出![]() 列联表,计算
列联表,计算![]() ,与临界值对比即可得出答案.
,与临界值对比即可得出答案.
(1)第二种生产方式的效率更高
理由如下:
解法一:由茎叶图可知:用第一种生产方式的工人中,有80%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有80%的工人完成生产任务所需时间至多78分钟,因此第二种生产方式的效率更高
解法二:由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为87分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟,因此第二种生产方式的效率更高
解法三:由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟,用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高
解法四:由茎叶图可知,用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布.又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成任务所需的时间更少,因此第二种生产方式的效率更高
以上四种理由,答出其中一种或其他合理理由均可.
(2)由茎叶图知![]()
列联表如下:
超过 | 不超过 | |
第一种生产方式 | 16 | 4 |
第二种生产方式 | 4 | 16 |
由于![]()
所以有99.9%的把握认为两种生产方式的效率有差异


科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为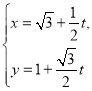 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上一点,
上一点,![]() 是曲线
是曲线![]() 上一点,求
上一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.

(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com