
| A. | $π-\frac{1}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{π}{4}+\frac{1}{3}$ | D. | $\frac{π}{2}-\frac{1}{3}$ |
分析 根据积分计算公式,求出被积函数的原函数,再根据微积分基本定理加以计算,即可得到本题答案.
解答 解:函数$f(x)=\left\{{\begin{array}{l}{{x^2},(x≤0)}\\{\sqrt{4-{x^2}}(x>0)}\end{array}}\right.$,
则$\int_{-1}^2{f(x)dx}$=${∫}_{-1}^{0}{x}^{2}dx$+${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx$=$\frac{1}{3}{x}^{3}{|}_{-1}^{0}$+$\frac{1}{4}π•{2}^{2}$=$π+\frac{1}{3}$,
故选B.
点评 本题求一个函数的原函数并求定积分值,考查定积分的运算和微积分基本定理等知识,属于基础题.


科目:高中数学 来源: 题型:选择题
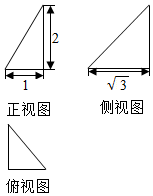 某几何体的三视图如图所示,则该几何体外接球的表面积为( )
某几何体的三视图如图所示,则该几何体外接球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{25π}{8}$ | C. | 12π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
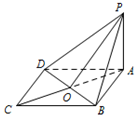
| A. | PD⊥CD | B. | BD⊥平面PAO | C. | PB⊥CB | D. | BC∥平面PAD |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{3},2]$ | B. | $[-\frac{1}{2},\frac{1}{2}]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和(万元) | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com