
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是  (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
【答案】
(1)解:曲线C的极坐标方程是ρ=2cosθ,化为ρ2=2ρcosθ,可得直角坐标方程:x2+y2=2x.
直线L的参数方程是  (t为参数),消去参数t可得
(t为参数),消去参数t可得 ![]()
(2)解:把  (t为参数),代入方程:x2+y2=2x化为:
(t为参数),代入方程:x2+y2=2x化为: ![]() +m2﹣2m=0,
+m2﹣2m=0,
由△>0,解得﹣1<m<3.
∴t1t2=m2﹣2m.
∵|PA||PB|=1=|t1t2|,
∴m2﹣2m=±1,
解得 ![]() ,1.又满足△>0.
,1.又满足△>0.
∴实数m=1 ![]() ,1.
,1.
【解析】(1)曲线C的极坐标方程是ρ=2cosθ,化为ρ2=2ρcosθ,利用 ![]() 可得直角坐标方程.直线L的参数方程是
可得直角坐标方程.直线L的参数方程是  (t为参数),把t=2y代入
(t为参数),把t=2y代入 ![]() +m消去参数t即可得出.(2)把
+m消去参数t即可得出.(2)把  (t为参数),代入方程:x2+y2=2x化为:
(t为参数),代入方程:x2+y2=2x化为: ![]() +m2﹣2m=0,由△>0,得﹣1<m<3.利用|PA||PB|=t1t2 , 即可得出.
+m2﹣2m=0,由△>0,得﹣1<m<3.利用|PA||PB|=t1t2 , 即可得出.


科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
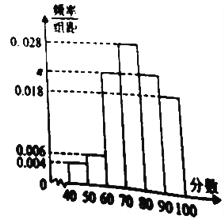
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式an=5﹣n,其前n项和为Sn , 将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn , 若存在m∈N* , 使对任意n∈N* , 总有Sn<Tn+λ恒成立,则实数λ的取值范围是( )
A.λ≥2
B.λ>3
C.λ≥3
D.λ>2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e﹣x(lnx﹣2k)(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与y轴垂直.
(1)求f(x)的单调区间;
(2)设 ![]() ,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
,对任意x>0,证明:(x+1)g(x)<ex+ex﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本![]() (万元)可以看出月产量
(万元)可以看出月产量![]() (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(I)写出月生产总成本![]() (万元)关于月产量
(万元)关于月产量![]() 吨的函数关系;
吨的函数关系;
(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“P数对”,设函数
的一个“P数对”,设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 。
。
(1)若![]() 是
是![]() 的一个“P数对”,且
的一个“P数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(2)若(1,1)是![]() 的一个“P数对”,且
的一个“P数对”,且![]() 在
在![]() 上单调递增,求函数
上单调递增,求函数![]() 在
在![]() 上的最大值与最小值;
上的最大值与最小值;
(3)若(-2,0)是![]() 的一个“P数对”,且当
的一个“P数对”,且当![]() 时,
时,![]() ,求k的值及
,求k的值及![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com