
 的等比数列,则|m-n|= .
的等比数列,则|m-n|= .  的等比数列的首项与末项的积等于第二项与第三项的积等于2,从而确定数列的每一项,再由两根之和分别为m、n,即可求出结果.
的等比数列的首项与末项的积等于第二项与第三项的积等于2,从而确定数列的每一项,再由两根之和分别为m、n,即可求出结果. 的等比数列
的等比数列 ,x4=
,x4=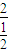 =4,公比为2∴x2=1,x3=2
=4,公比为2∴x2=1,x3=2 +4=
+4= ,n=x2+x3=1+2=3
,n=x2+x3=1+2=3 -3|=
-3|=


科目:高中数学 来源:2010年吉林省延边州图们二高中高三数学模拟训练试卷5(解析版) 题型:解答题
 的等比数列,则|m-n|= .
的等比数列,则|m-n|= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com