
分析 (1)利用导数求得函数h(x)的单调性,再求最值;
(2)方程f(x)=g(x)在[0,2]上恰有两个相异实根?F(x)=ex-2x-b在[0,2]上恰有两个相异实根?F(x)=ex-2x-b在[0,2]上与横轴有两个交点,利用导数求其单调性,利用图象即可,
(3)使f(x)的图象恒在g(x)图象上方?$?x∈R,p(x)=f(x)-g(x)={e^x}-\frac{a}{2}x+\frac{15}{2}>0$恒成立,求出p(x)的最小值即可.
解答 解:(1)$b=1-\frac{a}{2}$时,$h(x)={e^x}(\frac{a}{2}x+1-\frac{a}{2})(a∈R)$,∴h'(x)=ex(-2x+1),
当x$∈(0,\frac{1}{2})$时,h'(x)>0,当x($\frac{1}{2}$,1)时,h'(x)<0,
∴h(x)在[0,$\frac{1}{2}$]上递增,在($\frac{1}{2},1$)减,
$h{(x)_{max}}=h(\frac{1}{2})=2{e^{\frac{1}{2}}}$;
(2)F(x)=f(x)-g(x)=ex-2x-b,F'(x)=ex-2,
∴F(x)在(0,ln2)上单调递减;在(ln2,+∞)上单调递增;…(5分)
∴F(x)=ex-2x-b在[0,2]上恰有两个相异实根,
$?\left\{\begin{array}{l}F(0)=1-b≥0\\ F(ln2)=2-2ln2-b<0\\ F(2)={e^2}-4-b≥0\end{array}\right.?2-2ln2<b≤1$,
∴实数m的取值范围是m∈(2-2ln2,1]; …(7分)
(3)由题设:$?x∈R,p(x)=f(x)-g(x)={e^x}-\frac{a}{2}x+\frac{15}{2}>0$,(*)
∵$p'(x)={e^x}-\frac{a}{2}$,故p(x)在$(----∞,ln\frac{a}{2})$上单调递减;在$(ln\frac{a}{2},+∞)$上单调递增,
∴(*)$?p{(x)_{min}}=p(ln\frac{a}{2})=\frac{a}{2}-\frac{a}{2}ln\frac{a}{2}+\frac{15}{2}=\frac{1}{2}(a-aln\frac{a}{2}+15)>0$,
设$q(x)=x-xln\frac{x}{2}+15=x-x(lnx-ln2)+15$,则$q'(x)=1-ln\frac{x}{2}-1=-ln\frac{x}{2}$,
∴q(x)在(0,2)上单调递增;在(2,+∞)上单调递减,…(10分)
而q(2e2)=2e2-2e2lne2+15=15-2e2>0,
且$q(15)=15-15ln\frac{15}{2}+15=15(2-ln\frac{5}{2})=15(ln{e^2}-ln\frac{15}{2})<0$,
故存在${x_0}∈(2{e^2},15)$使q(x0)=0,
且x∈[2,x0)时h(x)>0,x∈(x0,+∞)时h(x)<0,
又∵$q(1)=16-ln\frac{1}{2}>0$,$7<{e^2}<\frac{15}{2}$,
∴a∈N*时使f(x)的图象恒在g(x)图象的上方的最大正整数a=14.…(12分)
点评 本题考查了导数的综合应用,转化思想是关键,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
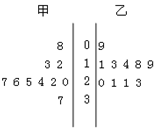 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )| A. | 甲的极差是29 | B. | 甲的中位数是25 | ||
| C. | 乙的众数是21 | D. | 甲的平均数比乙的大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
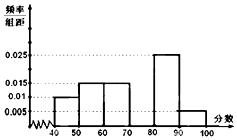 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
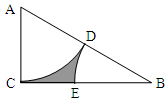 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | 1-$\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | 1-$\frac{π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com