
【题目】定义在 ![]() 上的奇函数
上的奇函数 ![]() 满足:
满足: ![]() ,且在区间
,且在区间 ![]() 上单调递减,则不等式
上单调递减,则不等式 ![]() 的解集是( )
的解集是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】∵定义在R上的奇函数f(x)在(0,+∞)上单调递减,且f(1)=0,∴函数f(x)在(﹣∞,0)上单调递减,且f(﹣1)=0,
∴不等式 ![]() 等价于
等价于 ![]() 或
或 ![]() ∴0<x<1或﹣1<x<0
∴0<x<1或﹣1<x<0
∴不等式xf(x)>0的解集为 ![]() .所以答案是:B
.所以答案是:B
【考点精析】根据题目的已知条件,利用函数的奇函数和解一元二次不等式的相关知识可以得到问题的答案,需要掌握一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数;求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,ABCD为正方形,过A作线段SA⊥平面ABCD,过A作与SC垂直的平面交SB,SC,SD于E,K,H,求证:E是点A在直线SB上的射影.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AB=AC=AA1 , AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 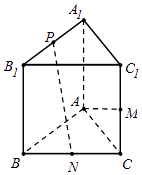
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数 ![]() 是偶函数,且满足
是偶函数,且满足 ![]() 上的解析式为
上的解析式为 ![]() ,过点
,过点 ![]() 作斜率为k的直线l , 若直线l与函数
作斜率为k的直线l , 若直线l与函数 ![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求倾斜角为直线y= ![]() +1的倾斜角的一半,且分别满足下列条件的直线方程:(1)
+1的倾斜角的一半,且分别满足下列条件的直线方程:(1)
【答案】解:∵直线l1:y= ![]() +1的斜率k1=
+1的斜率k1= ![]() ,
,
∴直线l1的倾斜角为120°,∴所求直线的倾斜角为60°,斜率k= ![]() .
.
∵过点(-4,1),∴直线方程为y-1= ![]() (x+4)
(x+4)
(1)经过点(-4,1)
(2)在y轴上的截距为-10.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com