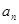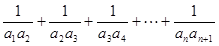已知：数列{a
n}的前n项和S
n=n
2+2n(n∈N
*)
（1）求：通项
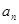
（2）求和：
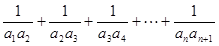
(1) a
n=" 2n+1;(2)"
.
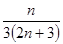
试题分析：（1）利用
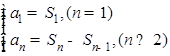
，即可求出结果；
（2）由于
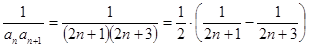
，所以求
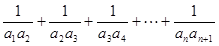
可以利用裂项相消法求和即可 .
试题解析：解：（Ⅰ）当n≥2时，a
n=S
n-S
n-1=2n+1, 2分
n=1时，a
1=S
1=3适合上式 3分
∴a
n=2n+1, n∈N
*, 4分
（Ⅱ）
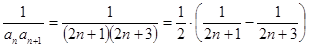
6分
∴原式
=
=
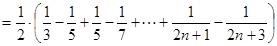
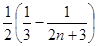
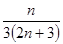
8分
练习册系列答案
相关习题
科目：高中数学
来源：不详
题型：解答题
已知等差数列
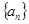
的前
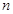
项和
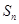
，且
,
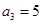
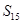
=225
（1）求数列
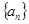
的通项公式；
（2）设
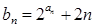
，求数列
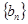
的前
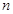
项和
.
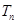
查看答案和解析>>
科目：高中数学
来源：不详
题型：解答题
已知数列
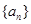
的前项和为
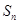
，且满足
；
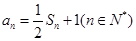
(Ⅰ)求数列
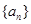
的通项公式；
(Ⅱ)若
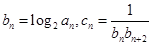
，且
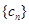
的前n项和为
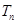
，求使得
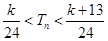
对
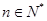
都成立的所有正整数k的值.
查看答案和解析>>
科目：高中数学
来源：不详
题型：填空题
已知等比数列{a
n}的前n项和为S
n，它的各项都是正数，且3a
1，
a3，2a2成等差数列，则
=______．
查看答案和解析>>
科目：高中数学
来源：不详
题型：填空题
若数列{a
n}是正项数列，且
＋
＋…＋
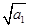
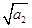
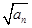
＝n
2＋3n(n∈N
*)，则
＋
＋…＋
＝________.
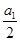
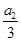
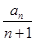
查看答案和解析>>
科目：高中数学
来源：不详
题型：解答题
设数列{
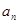
}是等差数列，数列{
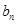
}的前
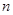
项和
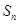
满足
,
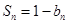
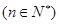
,且
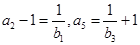
（1）求数列{
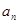
}和{
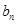
}的通项公式：
（2）设
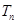
为数列{
．
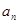
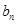
}的前
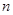
项和，求
．
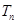
查看答案和解析>>
科目：高中数学
来源：不详
题型：解答题
在数列
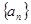
中，
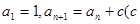
为常数，
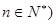
，且
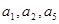
成公比不等于1的等比数列．
（1）求
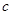
的值；
（2）设
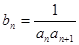
，求数列
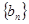
的前
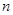
项和
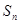
查看答案和解析>>
阅读快车系列答案
的前
项和为
，若
，则
等于
，且
，则
( )