
【题目】某上市公司股票在30天内每股的交易价格P(元)关于时间t(天)的函数关系为 ,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点
,该股票在30天内的日交易量Q(万股)关于时间t(天)的函数为一次函数,其图象过点![]() 和点
和点![]() .
.
(1)求出日交易量Q(万股)与时间t(天)的一次函数关系式;
(2)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
科目:高中数学 来源: 题型:
【题目】已知定直线![]() ,定点
,定点![]() ,以坐标轴为对称轴的椭圆
,以坐标轴为对称轴的椭圆![]() 过点
过点![]() 且与
且与![]() 相切.
相切.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)椭圆的弦![]() 的中点分别为
的中点分别为![]() ,若
,若![]() 平行于
平行于![]() ,则
,则![]() 斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.
斜率之和是否为定值? 若是定值,请求出该定值;若不是定值请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)一个袋子中装有4个大小形状完全相同的小球,球的编号分别为1,2,3,4,从袋中有放回的取两个球,设前后两次取得的球的编号分别为![]() 、
、![]() ,求
,求![]() 的概率;
的概率;
(2)某校早上![]() 开始上课,假设该校学生小张与小王在早上7:30~7:50之间到校,且每人在该时间段内到校时刻是等可能的,求小王比小张至少早5分钟到校的概率.
开始上课,假设该校学生小张与小王在早上7:30~7:50之间到校,且每人在该时间段内到校时刻是等可能的,求小王比小张至少早5分钟到校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到![]() 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为![]() ;当车流密度不超过
;当车流密度不超过![]() 辆/千米时,车流速度为
辆/千米时,车流速度为![]() 千米/小时,研究表明:当
千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·石家庄一模)祖暅是南北朝时期的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
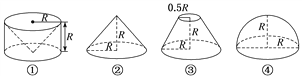
A. ①② B. ①③
C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别为
分别为![]() 的中点.有下述四个结论:①直线
的中点.有下述四个结论:①直线![]() 与直线
与直线![]() 垂直;②直线
垂直;②直线![]() 与平面
与平面![]() 平行;③平面
平行;③平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() ;④直线
;④直线![]() 与直线
与直线![]() 所成角的正切值为
所成角的正切值为![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )

A.②③B.②④C.①③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米 (四舍五入,精确到0.1米) 以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 ,第6小组的频数是7 .

(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记![]() 表示两人中进入决赛的人数,求
表示两人中进入决赛的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ) 经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )的焦点F,E上一点
)的焦点F,E上一点![]() 到焦点的距离为4.
到焦点的距离为4.
(1)求抛物线E的方程;
(2)过F作直线l交抛物线E于A,B两点,若直线AB中点的纵坐标为![]() ,求直线l的方程及弦
,求直线l的方程及弦![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com