
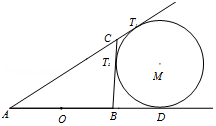
【题目】如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且 ![]() .固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系. 
(Ⅰ)求曲线Γ的方程;
(Ⅱ)设动直线l交曲线Γ于E、F两点,且以EF为直径的圆经过点O,求△OEF面积的取值范围.
【答案】解:(Ⅰ)依题意得AB=2,BD=1,设动圆M与边AC的延长线相切于T1 , 与边BC相切于T2 , 则AD=AT1 , BD=BT2 , CT1=CT2所以AD+BD=AT1+BT2=AC+CT1+BT2=AC+CT1+CT2=AC+BC=AB+2BD=4>AB=2
所以点C轨迹Γ是以A,B为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线Γ的方程为 ![]() .
.
(Ⅱ)由于曲线Γ要挖去长轴两个顶点,所以直线OE,OF斜率存在且不为0,所以可设直线 ![]()
由 ![]() 得
得 ![]() ,
, ![]() ,同理可得:
,同理可得: ![]() ,
, ![]() ;
;
所以 ![]() ,
, ![]()
又OE⊥OF,所以 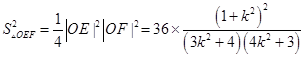
令t=k2+1,则t>1且k2=t﹣1,所以 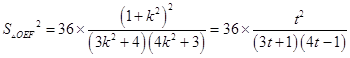 =
= 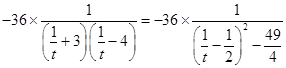
又 ![]() ,所以
,所以 ![]() ,所以
,所以 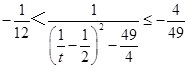 ,
,
所以 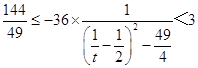 ,所以
,所以 ![]() ,
,
所以△OEF面积的取值范围为 ![]() .
.
【解析】(Ⅰ)确定点C轨迹Γ是以A,B为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点,即可求曲线Γ的方程;(Ⅱ)可设直线 ![]() ,进而表示面积,即可求△OEF面积的取值范围.
,进而表示面积,即可求△OEF面积的取值范围.


科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() ;
;
(2)已知结论:在直角三角形中,若两直角边长分别为![]() ,
,![]() ,斜边长为
,斜边长为![]() ,则斜边上的高
,则斜边上的高![]() .若把该结论推广到空间:在侧棱互相垂直的四面体
.若把该结论推广到空间:在侧棱互相垂直的四面体![]() 中,若三个侧面的面积分别为
中,若三个侧面的面积分别为![]() ,
,![]() ,
,![]() ,底面面积为
,底面面积为![]() ,则该四面体的高
,则该四面体的高![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 之间的关系是什么?(用
之间的关系是什么?(用![]() ,
,![]() ,
,![]() ,
,![]() 表示
表示![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ![]() )的周期为π,且图象上的一个最低点为M(
)的周期为π,且图象上的一个最低点为M(![]() ).
).
(1)求f(x)的解析式及单调递增区间;
(2)当x∈[0,![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘大学毕业生,经过综合测试,录用了14名女生和6名男生,这20名学生的测试成绩如茎叶图所示(单位:分),记成绩不小于80分者为![]() 等,小于80分者为
等,小于80分者为![]() 等.
等.

(1)求女生成绩的中位数及男生成绩的平均数;
(2)如果用分层抽样的方法从![]() 等和
等和![]() 等中共抽取5人组成“创新团队”,则从
等中共抽取5人组成“创新团队”,则从![]() 等和
等和![]() 等中分别抽几人?
等中分别抽几人?
(3)在(2)问的基础上,现从该“创新团队”中随机抽取2人,求至少有1人是![]() 等的概率.
等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() ;
;
(2)已知结论:在直角三角形中,若两直角边长分别为![]() ,
,![]() ,斜边长为
,斜边长为![]() ,则斜边上的高
,则斜边上的高![]() .若把该结论推广到空间:在侧棱互相垂直的四面体
.若把该结论推广到空间:在侧棱互相垂直的四面体![]() 中,若三个侧面的面积分别为
中,若三个侧面的面积分别为![]() ,
,![]() ,
,![]() ,底面面积为
,底面面积为![]() ,则该四面体的高
,则该四面体的高![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() 之间的关系是什么?(用
之间的关系是什么?(用![]() ,
,![]() ,
,![]() ,
,![]() 表示
表示![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com