Question

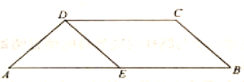
【题目】如图所示，在等腰梯形中，，，，点为的中点.将沿折起，使点到达的位置，得到如图所示的四棱锥，点为棱的中点.

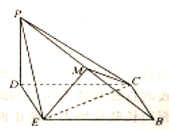
（1）求证：平面；

（2）若平面平面，求三棱锥的体积.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接，交于点，连接，易知底面是平行四边形，则为中点，又是中点，可知，则结论可证.

（2）先证明是等腰直角三角形，由条件中的面面垂直可得平面，则由（1）可知平面，则为三棱锥的高，底面的面积容易求得，根据公式求三棱锥的体积.

（1）在平面图中，

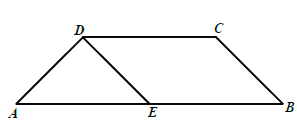
因为且，

所以四边形是平行四边形；

在立体图中，

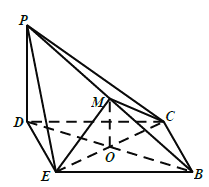
连接，交于点，连接，所以点是的中点，又因为点为棱的中点，

所以，因为平面，平面，

所以平面；

（2）在平面图中，

因为是平行四边形，所以，因为四边形是等腰梯形，

所以，所以，因为，所以；

在立体图中，，

又平面平面，且平面平面，平面

所以平面，

由（1）知，所以平面，

在等腰直角三角形中，因为，所以，

所以，又，

所以.