
【题目】已知![]() ,函数
,函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)根据函数![]() 解析式,先讨论当
解析式,先讨论当![]() 与
与![]() 两种情况.当
两种情况.当![]() 时易判断单调递减,当
时易判断单调递减,当![]() 时,讨论对称轴与区间
时,讨论对称轴与区间![]() 的关系,即可判断单调性.
的关系,即可判断单调性.
(2)根据(1)中所得![]() 在不同范围内的单调情况分类讨论. 当
在不同范围内的单调情况分类讨论. 当![]() ,
,![]() 在
在![]() 递减结合二次函数与绝对值函数的性质,并由
递减结合二次函数与绝对值函数的性质,并由![]() 的最大值即可求得
的最大值即可求得![]() 的值,进而得
的值,进而得![]() 的取值范围;当
的取值范围;当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减,同理解绝对值不等式可求得
递减,同理解绝对值不等式可求得![]() 的取值范围,进而得
的取值范围,进而得![]() 的取值范围.
的取值范围.
(1)①当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减
单调递减
②当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 单调递减
单调递减
③当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
④当![]() 时,不成立,所以无解.
时,不成立,所以无解.
综上所述,当![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
(2)①当![]() 时,
时,![]() 在
在![]() 递减,
递减,
![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
得![]() .
.
②当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
又![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴![]() ,同时
,同时![]() ,
,
∴![]()
∴
![]()
∴![]()
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]()
且可得![]() 在
在![]() 递增,
递增,
所以![]() .
.
综上所述, 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,母线长为
,母线长为![]() ,
,![]() ,
,![]() 、
、![]() 是底面半径,且:
是底面半径,且:![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,如图所示:
的中点,如图所示:
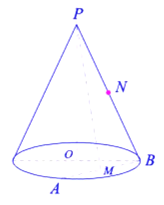
(1)求圆锥的表面积;
(2)求异面直线![]() 和
和![]() 所成的角的大小,并求
所成的角的大小,并求![]() 、
、![]() 两点在圆锥侧面上的最短距离.
两点在圆锥侧面上的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(Ⅰ)设直线![]() 被圆
被圆![]() 所截得的弦的中点为
所截得的弦的中点为![]() ,判断点
,判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)设圆![]() 被圆
被圆![]() 截得的一段圆弧(在圆
截得的一段圆弧(在圆![]() 内部,含端点)为
内部,含端点)为![]() ,若直线
,若直线![]() :
:![]() 与圆弧
与圆弧![]() 只有一个公共点,求实数
只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的纵坐标伸长到原来的
的图象上所有点的纵坐标伸长到原来的![]() 倍(横坐标不变),再向左平移
倍(横坐标不变),再向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,设函数
的图象,设函数![]() .
.
(1)对函数![]() 的解析式;
的解析式;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)若![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() ,
,![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+![]() ,过A作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.
,过A作AE⊥CD,垂足为E,现将△ADE沿AE折叠,使得DE⊥EC.

(1)求证:BC⊥面CDE;
(2)在线段AE上是否存在一点R,使得面BDR⊥面DCB,若存在,求出点R的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 点
点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]()
(1)求证; 平面![]() 平面
平面![]() ;
;
(2)若平面![]() 和平面
和平面![]() 的交线为
的交线为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点![]() 定义它们之间的一种“距离”:
定义它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() 上一点
上一点![]() 到点
到点![]() 的“距离”;
的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并求该“圆”围成的图形的面积;
的“圆”方程,并求该“圆”围成的图形的面积;
(3)若点![]() 到点
到点![]() 的“距离”和点
的“距离”和点![]() 到点
到点![]() 的“距离”相等,其中实数
的“距离”相等,其中实数![]() 满足
满足![]() ,求所有满足条件的点
,求所有满足条件的点![]() 的轨迹的长之和.
的轨迹的长之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com