
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为 ![]() ,短轴长为4
,短轴长为4 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为 ![]() .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为k1 , 直线PB的斜率为k2 , 判断k1+k2的值是否为常数,并说明理由.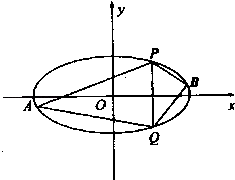
【答案】解:(Ⅰ)设椭圆C的方程为 ![]() . 由已知b=2
. 由已知b=2 ![]() ,离心率e=
,离心率e= ![]() ,a2=b2+c2 , 得a=4,
,a2=b2+c2 , 得a=4,
所以,椭圆C的方程为 ![]() .
.
(Ⅱ)①由(Ⅰ)可求得点P、Q的坐标为P(2,3),Q(2,﹣3),则|PQ|=6,
设A(x1 , y1),B(x2 , y2),直线AB的方程为y= ![]() x+t,代入
x+t,代入 ![]() ,
,
得:x2+tx+t2﹣12=0.
由△>0,解得﹣4<t<4,由根与系数的关系得 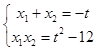 ,
,
四边形APBQ的面积 ![]() ,
,
故当t=0时, ![]() ;
;
②由题意知,直线PA的斜率 ![]() ,直线PB的斜率
,直线PB的斜率 ![]() ,
,
则 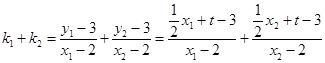
= 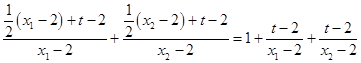
= ![]() ,
,
由①知 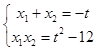 ,
,
可得 ![]() ,
,
所以k1+k2的值为常数0
【解析】(Ⅰ)设椭圆C的方程为 ![]() ,由短轴长可得b值,根据离心率为
,由短轴长可得b值,根据离心率为 ![]() 及a2=b2+c2 , 得a值; (Ⅱ)①设A(x1 , y1),B(x2 , y2),直线AB的方程为y=
及a2=b2+c2 , 得a值; (Ⅱ)①设A(x1 , y1),B(x2 , y2),直线AB的方程为y= ![]() x+t,代入
x+t,代入 ![]() 得x的二次方程,四边形APBQ的面积S=
得x的二次方程,四边形APBQ的面积S= ![]() =
= ![]() ,而|PQ|易求,代入韦达定理即可求得S的表达式,由表达式即可求得S的最大值;②直线PA的斜率
,而|PQ|易求,代入韦达定理即可求得S的表达式,由表达式即可求得S的最大值;②直线PA的斜率 ![]() ,直线PB的斜率
,直线PB的斜率 ![]() ,代入韦达定理即可求得k1+k2的值;
,代入韦达定理即可求得k1+k2的值;
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣8y+12=0,直线l经过点D(﹣2,0),且斜率为k.
(1)求以线段CD为直径的圆E的方程;
(2)若直线l与圆C相离,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省每年损失耕地20万亩,每亩耕地价值24000元,为了减少耕地损失,决定按耕地价格的t%征收耕地占用税,这样每年的耕地损失可减少 ![]() t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
t万亩,为了既可减少耕地的损失又保证此项税收一年不少于9000万元,则t的取值范围是( )
A.[1,3]
B.[3,5]
C.[5,7]
D.[7,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且 ![]() .
.
(1)求证:△ABC是直角三角形;
(2)设圆O过A,B,C三点,点P位于劣弧AC上,∠PAB=60°,求四边形ABCP的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,椭圆与y轴的正半轴交于点B,且|BF|=
,右焦点为F,椭圆与y轴的正半轴交于点B,且|BF|= ![]() .
.
(1)求椭圆E的方程;
(2)若斜率为1的直线l经过点(1,0),与椭圆E相交于不同的两点M,N,在椭圆E上是否存在点P,使得△PMN的面积为 ![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,已知a1=2,b1=4,且﹣an , bn , an+1成等差数列,﹣bn , an , bn+1也成等差数列. (Ⅰ)求证:数列{an+bn}和{an﹣bn}都是等比数列,并求数列{an}的通项公式;
(Ⅱ)若cn=(an﹣3n)log3[an﹣(﹣1)n],求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是单位圆上的两点,O为圆心,且∠AOB=90°,MN是圆O的一条直径,点C在圆内,且满足 ![]() =λ
=λ ![]() +(1﹣λ)
+(1﹣λ) ![]() (λ∈R),则
(λ∈R),则 ![]()
![]() 的最小值为( )
的最小值为( )
A.﹣ ![]()
B.﹣ ![]()
C.﹣ ![]()
D.﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com