
已知向量![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),
=(x2,y2),![]() =(x3,y3),定义运算“*”的意义为
=(x3,y3),定义运算“*”的意义为![]() *
*![]() =(x1y2,x2y1).则下列命题①若
=(x1y2,x2y1).则下列命题①若![]() =(1,2),
=(1,2),![]() =(3,4),则
=(3,4),则![]() *
*![]() =(6,4)
=(6,4)
②![]() *
*![]() =
=![]() *
*![]()
③(![]() *
*![]() )*
)*![]() =
=![]() *(
*(![]() *
*![]() )
)
④(![]() +
+![]() )*
)*![]() =(
=(![]() *
*![]() )+(
)+(![]() *
*![]() )中,正确的是________.
)中,正确的是________.
科目:高中数学 来源:南通高考密卷·数学(理) 题型:044
已知向量p=(a,x+1),q=(x,a),m=(1,y),且(p-q)∥m,y与x的函数关系式为y=f(x).
(1)求f(x);
(2)判断并证明函数y=f(x)当x>a时的单调性;
(3)我们利用函数y=f(x)构造一个数列{xn),方法如下:对于f(x)定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),….在上述构造数列的过程中,如果xi(i=1,2,3,4,…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.如果取f(x)定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的值.
查看答案和解析>>
科目:高中数学 来源:2007年福建省厦门市普通中学高中毕业班质量检查数学(理科)试题 题型:044
已知向量a=(1,1),b=(1,0),c满足a·c=0且|a|=|c|,b·c>0.
(1)求向量c;
(2)若映射f:(x,y)→(x1,y1)=xa+yc,求映射f下(1,2)的原象.
查看答案和解析>>
科目:高中数学 来源:“伴你学”新课程 数学·必修3、4(人教B版) 人教B版 题型:047
已知两点A(x1,y1),B(x2,y2),试用向量的方法证明以线段AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知向量i=(1,0),j=(0,1),对坐标平面内的任一向量a,给出下列四个结论:
①存在唯一的一对实数x、y,使得a=(x,y);
②若x1,y1,x2,y2∈R,a=(x1,y1)≠(x2,y2),则x1≠x2,且y1≠y2;
③若x,y∈R,a≠0,且a=(x,y),则a的起点是原点O;
④若x,y∈R,a≠0,且a的终点的坐标是(x,y),则a=(x,y).
在以上四个结论中,正确的结论共有
查看答案和解析>>
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点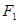 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com