
【题目】已知函数![]()
(Ⅰ)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上是减函数,且对任意的
上是减函数,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)2(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题分析:(I)由函数f(x)的解析式,可得函数在(-∞,a]上单调递减,进而得到f(x)在[1,a]上单调递减,则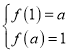 ,由此构造关于a的方程组,解之可得答案.(Ⅱ)若f(x)在区间(-∞,2]上是减函数,则(-∞,2](-∞,a],进而结合x∈[1,a+1]时,f(x)max=f(1),构造关于a的不等式,解不等式,可得答案.(III)由函数g(x)在[0,1]上递增,f(x)在[0,1]上递减,可分别求出两个函数的值域,若对任意的x∈[0,1],都存在x0∈[0,1],使得f(x0)=g(x)成立;则两个函数的值域满足:[1,3][6-2a,5],进而可得答案
,由此构造关于a的方程组,解之可得答案.(Ⅱ)若f(x)在区间(-∞,2]上是减函数,则(-∞,2](-∞,a],进而结合x∈[1,a+1]时,f(x)max=f(1),构造关于a的不等式,解不等式,可得答案.(III)由函数g(x)在[0,1]上递增,f(x)在[0,1]上递减,可分别求出两个函数的值域,若对任意的x∈[0,1],都存在x0∈[0,1],使得f(x0)=g(x)成立;则两个函数的值域满足:[1,3][6-2a,5],进而可得答案
试题解析:(Ⅰ)∵![]()
∴![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]()
(Ⅱ)∵![]() 在区间
在区间![]() 上是减函数, ∴
上是减函数, ∴![]() ∴
∴![]()
∴![]() ,
,![]()
∴![]() 时,
时,![]()
又∵对任意的![]() ,都有
,都有![]() ,
,
∴![]() , 即
, 即 ![]() , ∴
, ∴![]()
(Ⅲ)∵![]() 在
在![]() 上递增,
上递增,![]() 在
在![]() 上递减,
上递减,
当![]() 时,
时,![]() ,
,![]()
∵对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立;
成立;
∴![]()
![]()
∴![]()
![]()


科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
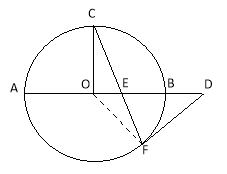
(1)求证:DE2=DBDA;
(2)若DB=2,DF=4,试求CE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本
(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本![]() 固定成本+生产成本),销售收入
固定成本+生产成本),销售收入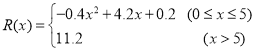 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入—总成本);
销售收入—总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,圆
,圆![]() 是以
是以![]() 的中点为圆心,
的中点为圆心,![]() 为半径的圆.
为半径的圆.
(1)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;
(2)若![]() 是圆
是圆![]() 外一点,从
外一点,从![]() 向圆
向圆![]() 引切线
引切线![]() ,
,![]() 为切点,
为切点,![]() 为坐标原点,
为坐标原点,![]() ,求使
,求使![]() 最小的点
最小的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中,正确的个数是( )
(1){0}∈{0,1,2};(2){0,1,2}{2,1,0};(3) {0,1,2}.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题,若某地区2015年人口总数为![]() 万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加
万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加![]() 万人,从2026年开始到2035年每年人口为上一年的
万人,从2026年开始到2035年每年人口为上一年的![]() .
.
(1)求实施新政策后第![]() 年的人口总数
年的人口总数![]() 的表达式(注:2016年为第一年);
的表达式(注:2016年为第一年);
(2)若新政策实施后的2016年到2035年人口平均值超过![]() 万,则需调整政策,否则继续实施,问到2035年后是否需要调整政策?(说明:
万,则需调整政策,否则继续实施,问到2035年后是否需要调整政策?(说明:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com