考点:数列的函数特性
专题:等差数列与等比数列
分析:由图象可知可能:①a7=0.7,S7=-0.8,a8=-0.4.②a7=0.7,S7=-0.8,S8=-0.4.③a7=-0.8,S7=0.7,a8=-0.4.④a7=-0.8,S7=0.7,S8=-0.4.分别利用等差数列的通项公式及其前n项和公式即可判断出.
解答:
解:由图象可知可能:①a
7=0.7,S
7=-0.8,a
8=-0.4,由a
7=0.7,a
8=-0.4,可得d=-1.1,a
1=7.3.
∴S
7=
>0,与S
7=-0.8,矛盾,舍去.
②a
7=0.7,S
7=-0.8,S
8=-0.4.由S
7=-0.8,S
8=-0.4,可得a
8=0.4,∴
=-0.4,解得a
1=-0.5,∴a
8=-0.5+7d,解得d=
≠0.4-0.7=-0.3,矛盾,舍去.
③a
7=-0.8,S
7=0.7,a
8=-0.4.由a
7=-0.8,S
7=0.7,可得
=0.7,解得a
1=1,∴-0.8=1+6d,解得d=-0.3,而-0.4-(-0.8)=0.4,矛盾,舍去.
④a
7=-0.8,S
7=0.7,S
8=-0.4.由a
7=-0.8,S
7=0.7,可得
=0.7,解得a
1=1.
∴-0.8=1+6d,解得d=-0.3,∴a
8=-0.8-0.3=-1.1,∴S
8=0.7-1.1=-0.4,满足条件.
∴a
n=a
1+(n-1)d=1-0.3(n-1)=1.3-0.3n≥0,解得
n≤=4+
,
因此当n=4时,S
n取得最大值.
故选:A.
点评:本题考查了等差数列的通项公式及其前n项和公式,考查了数形结合的思想方法、分类讨论的方法,考查了推理能力与计算能力,属于难题.

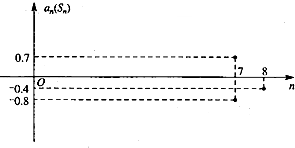 设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )
设等差数列{an}的前n项和为Sn,在同一个坐标系中,an=f(n)及Sn=g(n)的部分图象如图所示,则( )
