
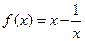
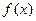 )在区间
)在区间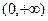 的单调性;
的单调性;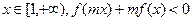 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:不详 题型:解答题
 年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图: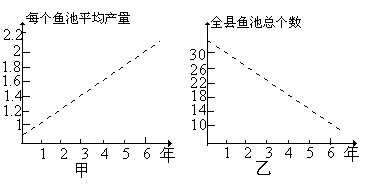
 年
年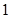 万只鳗鱼上升到第
万只鳗鱼上升到第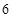 年
年 万只。
万只。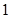 年
年 个减少到第
个减少到第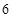 年
年 个。
个。 年全县鱼池的个数及全县出产的鳗鱼总数;
年全县鱼池的个数及全县出产的鳗鱼总数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
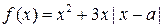 ,其中
,其中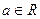 ,
,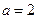 时,把函数
时,把函数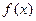 写成分段函数的形式;
写成分段函数的形式;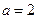 时,求
时,求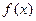 在区间
在区间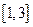 上的最值;
上的最值;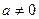 ,函数
,函数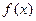 在
在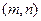 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出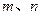 的取值范围(用
的取值范围(用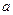 表示).
表示).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
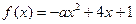 的定义域为[-1,2],
的定义域为[-1,2],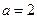 ,求函数
,求函数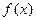 的值域;(6分)
的值域;(6分) 为非负常数,且函数
为非负常数,且函数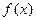 是[-1,2]上的单调函数,求
是[-1,2]上的单调函数,求 的范围及函数
的范围及函数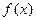 的值域。(6分)
的值域。(6分)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 种方案时第一台收割机投入工作的时间为 小时.
种方案时第一台收割机投入工作的时间为 小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com