
分析 (Ⅰ)求出函数的导数,通过讨论a得到范围,求出函数的单调区间即可;
(Ⅱ)由f(x)=ex-ax-a,f'(x)=ex-a,从而化恒成立问题为最值问题,讨论求实数a的取值范围.
解答 解:(Ⅰ)f(x)=ex-ax,f′(x)=ex-a,
当a≤0时,f′(x)>0,则f(x)在R上单调递增;
当a>0时,令f′(x)=ex-a=0,得x=lna,
则在(-∞,lna]上单调递减,在(lna,+∞)上单调递增;
(Ⅱ)由f(x)=ex-ax,f'(x)=ex-a,
若a<0,则f'(x)>0,函数f(x)单调递增,
当x趋近于负无穷大时,f(x)趋近于负无穷大;
当x趋近于正无穷大时,f(x)趋近于正无穷大,
故a<0不满足条件.
若a=0,f(x)=ex≥0恒成立,满足条件.
若a>0,由f'(x)=0,得x=lna,
当x<lna时,f'(x)<0;当x>lna时,f'(x)>0,
所以函数f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
所以函数f(x)在x=lna处取得极小值f(lna)=elna-a•lna=a-a•lna,
由f(lna)≥0得a-a•lna≥0,
解得0<a≤e.
综上,满足f(x)≥0恒成立时实数a的取值范围是[0,e].
点评 本题考查了导数的综合应用及恒成立问题,属于中档题.


科目:高中数学 来源: 题型:选择题
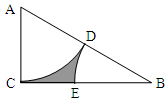 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | 1-$\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | 1-$\frac{π}{4}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
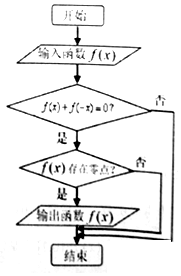 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x4 | C. | f(x)=2x | D. | f(x)=x-$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{bn}是等差数列,{bn}的公差也为d | |
| B. | 数列{bn}是等差数列,{bn}的公差为2d | |
| C. | 数列{an+bn}是等差数列,{an+bn}的公差为d | |
| D. | 数列{an-bn}是等差数列,{an-bn}的公差为$\frac{d}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com