
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+1+2n﹣3.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
【答案】
(1)解:∵2Sn=3n+1+2n﹣3,
∴当n≥2时,2an=2Sn﹣2Sn﹣1=(3n+1+2n﹣3)﹣[3n+2(n﹣1)﹣3]=23n+2,
∴an=3n+1,
又a1=S1= ![]() (32+2×1﹣3)=4,适合上式,
(32+2×1﹣3)=4,适合上式,
∴an=3n+1;
(2)解:由(1)知an=3n+1,则nan=n3n+n,
∵数列{nan}的前n项和Tn,
则Tn=131+232+…+n3n+(1+2+3+…+n),
令An=131+232+…+n3n,①
则3An=132+233+…+(n﹣1)3n+n3n+1,②
①﹣②得:﹣2An=31+32+…+3n﹣n3n+1
= ![]() ﹣n3n+1=(
﹣n3n+1=( ![]() )3n+1﹣
)3n+1﹣ ![]() ,
,
∴An= ![]() 3n+1+
3n+1+ ![]() .
.
∴Tn= ![]() 3n+1+
3n+1+ ![]() +
+ ![]()
【解析】(1)由Sn=3n+1+2n﹣3,可得当n≥2时,an=Sn﹣Sn﹣1=3n+1,再检验当n=1时,a1是否适合上式,即可求得数列{an}的通项公式;(2)依题意,nan=n3n+n,Tn=131+232+…+n3n+(1+2+3+…+n),令An=131+232+…+n3n , 利用错位相减法可求得An= ![]() 3n+1+
3n+1+ ![]() ,而1+2+3+…+n=
,而1+2+3+…+n= ![]() ,从而可得数列{nan}的前n项和Tn .
,从而可得数列{nan}的前n项和Tn .
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系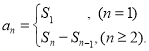 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径,若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点.
(1)求圆A的方程;
(2)当|MN|=2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表:
ωx+φ | 0 |
| π |
| 2π |
x | π |
| |||
Asin(ωx+φ) | 0 | 3 | ﹣3 | 0 |
(1)请将上表空格中处所缺的数据填写在答题卡的相应位置上,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点的横坐标缩短为原来的 ![]() ,再将所得图象向左平移
,再将所得图象向左平移 ![]() 个单位,得到y=g(x)的图象,求g(x)的单调递增区间.
个单位,得到y=g(x)的图象,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
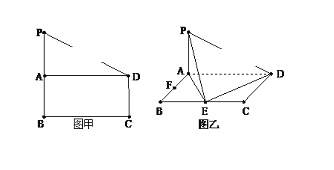
【题目】如图甲,在直角梯形PBCD中,PB∥CD,CD⊥BC,BC=PB=2CD,A是PB的中点.
现沿AD把平面PAD折起,使得PA⊥AB(如图乙所示),E、F分别为BC、AB边的中点.
(1)求证:平面PAE⊥平面PDE;
(2)在PE上找一点Q,使得平面BDQ⊥平面ABCD.
(3)在PA上找一点G,使得FG∥平面PDE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com