
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(![]() )证明数列
)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式.
的通项公式.
(![]() )设
)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(![]() )数列
)数列![]() 中是否存在三项,它们可以构成等比数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等比数列?若存在,求出一组符合条件的项;若不存在,说明理由.
【答案】(1)![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】分析:(1)先根据和项与通项关系得![]() , 再代入化简
, 再代入化简![]() 得2,最后根据等比数列定义以及通项公式求数列
得2,最后根据等比数列定义以及通项公式求数列![]() 的通项公式.(2)由于
的通项公式.(2)由于![]() ,再利用错位相减法求和
,再利用错位相减法求和![]() ,(3)先)假设存在
,(3)先)假设存在![]() ,
,![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列,化简利用奇偶分析法得
成等比数列,化简利用奇偶分析法得![]() ,与
,与![]() 矛盾,因此不存在.
矛盾,因此不存在.
详解:解:(![]() )数列
)数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
两式相减得:![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
又当![]() 时,
时,![]() ,得
,得![]() ,
,
∴数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,
,
∴![]() .
.
(![]() )由题意,
)由题意,![]() ,
,
∴![]() ,
,
![]() ,
,
两式相减得![]()
![]()
![]()
![]()
![]()
![]() .
.
(![]() )假设存在
)假设存在![]() ,
,![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是奇数,
是奇数,![]() ,
,![]() 也是奇数,
也是奇数,
∴![]() 是奇数,
是奇数,
![]() 是奇数,即
是奇数,即![]()
故![]() ,因此
,因此![]() ,与
,与![]() 矛盾
矛盾
故数列![]() 中不存在三项,可以构成等比数列.
中不存在三项,可以构成等比数列.


科目:高中数学 来源: 题型:
【题目】选修4—5:不等式选讲
已知函数(x)=|2x-a|+ |x -1|.
(Ⅰ)当a=3时,求不等式(x)≥2的解集;
(Ⅱ)若(x)≥5-x对![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
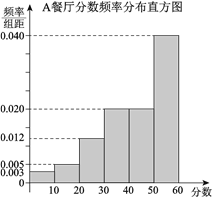
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一牧羊人赶着一群羊通过4个关口,每过一个关口,守关人将拿走当时羊的一半,然后退还一只给牧羊人,过完这些关口后,牧羊人只剩下3只羊,则牧羊人在过第1个关口前有_________只羊.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com