
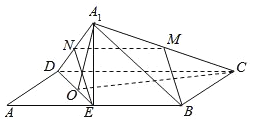
【题目】如图,在矩形ABCD中,![]() ,E为AB的中点.将
,E为AB的中点.将![]() 沿DE翻折,得到四棱锥
沿DE翻折,得到四棱锥![]() .设
.设![]() 的中点为M,在翻折过程中,有下列三个命题:
的中点为M,在翻折过程中,有下列三个命题:
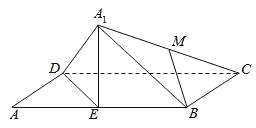
①总有![]() 平面
平面![]() ;
;
②线段BM的长为定值;
③存在某个位置,使DE与![]() 所成的角为90°.
所成的角为90°.
其中正确的命题是_______.(写出所有正确命题的序号)
【答案】①②
【解析】
取![]() D的中点N,连接MN,EN,根据四边形MNEB为平行四边形判断①,②,假设DE⊥
D的中点N,连接MN,EN,根据四边形MNEB为平行四边形判断①,②,假设DE⊥![]() C得出矛盾结论判断③.
C得出矛盾结论判断③.
取![]() D的中点N,连接MN,EN,
D的中点N,连接MN,EN,
则MN为△![]() CD的中位线,
CD的中位线,
∴MN∥![]() CD,且MN=
CD,且MN=![]() CD
CD
又E为矩形ABCD的边AB的中点,∴BE∥![]() CD,且BE=
CD,且BE=![]() CD
CD
∴MN∥BE,且MN=BE即四边形MNEB为平行四边形,∴BM∥EN,
又EN平面A1DE,BM平面A1DE,
∴BM∥平面![]() DE,故①正确;
DE,故①正确;
由四边形MNEB为平行四边形可得BM=NE,
而在翻折过程中,NE的长度保持不变,故BM的长为定值,故②正确;
取DE的中点O,连接![]() O,CO,
O,CO,
由![]() D=
D=![]() E可知
E可知![]() O⊥DE,
O⊥DE,
若DE⊥![]() C,则DE⊥平面
C,则DE⊥平面![]() OC,
OC,
∴DE⊥OC,又∠CDO=90°﹣∠ADE=45°,
∴△OCD为等腰直角三角形,故而CD![]() OD,
OD,
而OD![]() DE
DE![]() ,CD=4,与CD
,CD=4,与CD![]() OD矛盾,故DE与
OD矛盾,故DE与![]() C所成的角不可能为90°.
C所成的角不可能为90°.
故③错误.
故答案为:①②.


科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,过点
中,过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() ,若
,若![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列,
为公比的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
(3)设函数![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() 函数
函数![]() 的图像关于直线
的图像关于直线![]() 对称,当方程
对称,当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
X | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,+∞) |
人数 | t | 1 | 1 | 1 | 1 | 1 |
依据上述材料回答下列问题:
(1)求t的值;
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
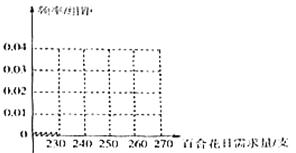
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间两条互相垂直的直线,等腰直角三角形![]() 的直角边
的直角边![]() 所在直线与a,b都垂直,斜边
所在直线与a,b都垂直,斜边![]() 以
以![]() 为旋转轴选择,有下列结论:
为旋转轴选择,有下列结论:
①当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成30°角;
与b成30°角;
②当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成60°角;
与b成60°角;
③直线![]() 与a所成角的最小值为45°;
与a所成角的最小值为45°;
④直线![]() 与a所成角的最大值为60°;
与a所成角的最大值为60°;
其中正确的是_______.(填写所以正确结论的编号).
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
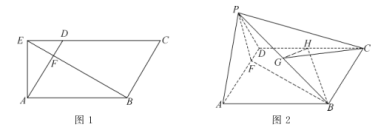
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在经过点![]() 的直线
的直线![]() ,它与椭圆
,它与椭圆![]() 相交于
相交于![]() 两个不同点,且满足
两个不同点,且满足![]() 为坐标原点)关系的点
为坐标原点)关系的点![]() 也在椭圆
也在椭圆![]() 上,如果存在,求出直线
上,如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]() ,
,![]() .如果集合
.如果集合![]() 满足:对于任意的
满足:对于任意的![]() ,都有
,都有![]() ,那么称集合
,那么称集合![]() 具有性质
具有性质![]() .
.
(Ⅰ)写出一个具有性质![]() 的集合
的集合![]() ;
;
(Ⅱ)证明:对任意具有性质![]() 的集合
的集合![]() ,
,![]() ;
;
(Ⅲ)求具有性质![]() 的集合
的集合![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.
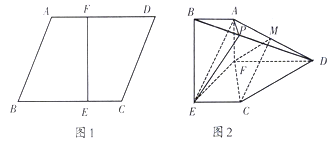
(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com