
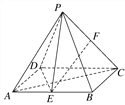
【题目】如图,四棱锥P-ABCD的底面为矩形,AB=![]() ,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
(1)求证:EF∥平面PAD;
(2)求证:平面PAC⊥平面PDE.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)取PD中点G,根据平几知识可得AEFG为平行四边形,即得EF∥AG,再根据线面平行判定定理得结论(2)由矩形性质得DE⊥AC.又DE⊥PA.因此由线面垂直判定定理得DE⊥平面PAC.再根据面面垂直判定定理得结论
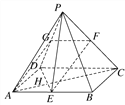
试题解析:证明 (1)如图,取PD中点G,连接AG,FG,
因为F,G分别为PC,PD的中点,所以FG∥CD,且FG=![]() CD.
CD.
又因为E为AB中点,所以AE∥CD,且AE=![]() CD.
CD.
所以AE∥FG,AE=FG.
所以四边形AEFG为平行四边形.
所以EF∥AG,又EF平面PAD,
AG平面PAD,
所以EF∥平面PAD.
(2)设AC∩DE=H,由△AEH∽△CDH及E为AB中点,得![]() =
=![]() =
=![]() ,
,
又因为AB=![]() ,BC=1,
,BC=1,
所以AC=![]() ,AH=
,AH=![]() AC=
AC=![]() .
.
所以![]() =
=![]() =
=![]() ,又∠BAC为公共角,所以△HAE∽△BAC.
,又∠BAC为公共角,所以△HAE∽△BAC.
所以∠AHE=∠ABC=90°,
即DE⊥AC.
又DE⊥PA,PA∩AC=A,PA平面PAC,AC平面PAC,所以DE⊥平面PAC.
又DE平面PDE,
所以平面PAC⊥平面PDE.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() 上任意一点,点
上任意一点,点![]() 与点
与点![]() 关于原点对称,线段
关于原点对称,线段![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
,![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于
交于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使以
,使以![]() 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[-1,1]上的奇函数,在[0,1]上f(x)=2x+ln(x+1)-1.
(1)求函数f(x)的解析式;并判断f(x)在[-1,1]上的单调性(不要求证明);
(2)解不等式f(2x-1)+f(1-x2)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
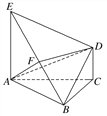
【题目】如图所示,底面ABC为正三角形,EA⊥平面ABC,DC⊥平面ABC,EA=AB=2DC=2a,设F为EB的中点.
(1)求证:DF∥平面ABC;
(2)求直线AD与平面AEB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() ,
, ![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() :
: ![]() (
(![]() ,
, ![]() )的一条直径的两个端点.
)的一条直径的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 与椭圆
与椭圆![]() 分别相交于
分别相交于![]() 、
、![]() .试探究:是否存在数集
.试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且tan∠EAB=![]() .
.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE,证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com