
【题目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展开式中,把D
x2n的展开式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三项式系数
叫做三项式系数
(1)求D ![]() 的值
的值
(2)根据二项式定理,将等式(1+x)2n=(1+x)n(x+1)n的两边分别展开可得,左右两边xn的系数相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,请计算D
)2 , 利用上述思想方法,请计算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
【答案】
(1)解:令x=1,则D40+D41+D42+D43+D44+D45+D46+D47+D48=34=81,
令x=﹣1,则D40﹣D41+D42﹣D43+D44﹣D45+D46﹣D47+D48=(1﹣1+1)4=1,
∴D ![]()
= ![]() [(D40+D41+D42+D43+D44+D45+D46+D47+D48)
[(D40+D41+D42+D43+D44+D45+D46+D47+D48)
+(D40﹣D41+D42﹣D43+D44﹣D45+D46﹣D47+D48)]= ![]() ×(81+1)=41
×(81+1)=41
(2)解:∵(1+x+x2)2017 =D20170+D20171x+D20172x2+…+D2017rxr+…+D20174033x4033+D20174034x4034,
(x﹣1)2017 =C20170x2017﹣C20171x2016+C20172x2015﹣C20173x2015+…+﹣C20172016x+C20172017,
其中其中x2017系数为D20170C20170﹣D20171C20171+D20172C20172﹣D20173C20173+…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]()
∵(1+x+x2)2017 (x﹣1)2017=(x3﹣1)2017,
而二项式的(x3﹣1)2017的通项公式 Tr+1=C2017r(﹣1)r(x3)2017﹣r,
因为2017不是3的倍数,所以(x3﹣1)2017的展开式中没有x2017项,由代数式恒成立,
D20170C20170﹣D20171C20171+D20172C20172﹣D20173C20173+…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() =0
=0
【解析】(1)分别根据新定义,令x=1或x=﹣1,即可求出答案,(2)根据(1+x+x2)2017 (x﹣1)2017 =(x3﹣1)2017的等式两边的x2017项的系数相同,从求得要求式子的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某球星在三分球大赛中命中率为 ![]() ,假设三分球大赛中总计投出8球,投中一球得3分,投丢一球扣一分,则该球星得分的期望与方差分别为( )
,假设三分球大赛中总计投出8球,投中一球得3分,投丢一球扣一分,则该球星得分的期望与方差分别为( )
A.16,32
B.8,32
C.8,8
D.32,32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖,又叫属相,是中国与十二地支相配以人出生年份的十二种动物,包括鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。已知在甲、乙、丙、丁、戊、己六人中,甲、乙、丙的属相均是龙,丁、戊的属相均是虎,己的属相是猴,现从这六人中随机选出三人,则所选出的三人的属相互不相同的概率等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
![]() 且
且![]() .
.
(1)当![]() 时,设集合
时,设集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的条件下,若![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只小船以![]() 的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以
的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以![]() 的速度前进(如图),现在小船在水平面上的
的速度前进(如图),现在小船在水平面上的![]() 点以南的40米处,汽车在桥上
点以南的40米处,汽车在桥上![]() 点以西的30米处(其中
点以西的30米处(其中![]() 水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).
水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
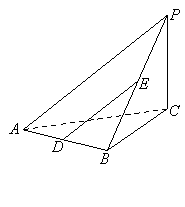
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}的通项公式分别是an=(﹣1)n+2016a,bn=2+ ![]() ,若an<bn , 对任意n∈N+恒成立,则实数a的取值范围是 .
,若an<bn , 对任意n∈N+恒成立,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x0∈R,x02﹣2x0+3≤0的否定是x∈R,x2﹣2x+3>0,命题q:双曲线 ![]() ﹣y2=1的离心率为2,则下列命题中为真命题的是( )
﹣y2=1的离心率为2,则下列命题中为真命题的是( )
A.p∨q
B.¬p∧q
C.¬p∨q
D.p∧q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com