
���� ���������ں����Ķ��壬�ֱ�����жϼ��ɣ�
��� �⣺������������ں�����y=f��x���ġ������ڡ�Ϊ-1��
��f��x-1��=-f��x������f��x-1��=-f��x��=-��-f��x+1����=f��x+1����
����������Ϊ2�����ں������ʢ���ȷ����
�ڶ��ڡ������ڡ�ΪT�ĺ���y=f��x������f��T����0����f��2015T��=T2014��f��T����0���ʢ���ȷ��
��������f��x��=x�ǡ������ں�������
����ڷ��㳣��T��ʹf��x+T��=T•f��x����
��x+T=Tx���ʣ�1-T��x+T=0�������
�ʲ�����T���ʼ��費�������ʢ۴���
��������f��x��=2-x�ǡ������ں�������
����ڷ��㳣��T��ʹf��x+T��=T•f��x����
��2-x-T=T•2-x��
����T-2-T��•2-x=0��
����y=x-2-x����ͼ�����£�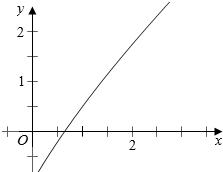
�ʴ���T��0��ʹT-2-T=0���ʢ���ȷ��
��������f��x��=cos��x�ǡ������ں�������
����ڷ��㳣��T��ʹf��x+T��=T•f��x����
��cos����x+��T��=Tcos��x��
��T=1��T=-1��
�ʡ���=k�У�k��Z�����ʢ���ȷ��
�ʴ�Ϊ���٢ڢܢݣ�
���� ������Ҫ�����뺯���йص����������жϣ���ȷ���������ں����Ķ����ǽ������Ĺؼ���


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-1��x��1} | B�� | {x|x��0} | C�� | {x|0��x��1} | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com