
【题目】已知函数f(x)=sinωx﹣ ![]() cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣ax+(3﹣a)lnx,a∈R.
x2﹣ax+(3﹣a)lnx,a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线2x﹣y+1=0垂直,求a的值;
(2)设f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:﹣5﹣f(x1)<f(x2)<﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
: ![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.
两点.

(1)若直线![]() ,
, ![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点;
过定点;
(2)若线段![]() 的中点
的中点![]() 在曲线
在曲线![]() :
: ![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P为正方体ABCD﹣A1B1C1D1中AC1与BD1的交点,则△PAC在该正方体各个面上的射影可能是( ) 
A.①②③④
B.①③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0),其准线方程为x+1=0,直线l过点T(t,0)(t>0)且与抛物线交于A、B两点,O为坐标原点.
(1)求抛物线方程,并证明: ![]()
![]() 的值与直线l倾斜角的大小无关;
的值与直线l倾斜角的大小无关;
(2)若P为抛物线上的动点,记|PT|的最小值为函数d(t),求d(t)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,已知建筑第5层楼房时,每平方米建筑费用为
万元,已知建筑第5层楼房时,每平方米建筑费用为![]() 万元.
万元.
![]() 若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和
若学生宿舍建筑为x层楼时,该楼房综合费用为y万元,综合费用是建筑费用与购地费用之和![]() ,写出
,写出![]() 的表达式;
的表达式;
![]() 为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn(n∈N*),且满足: ①|a1|≠|a2|;
②r(n﹣p)Sn+1=(n2+n)an+(n2﹣n﹣2)a1 , 其中r,p∈R,且r≠0.
(1)求p的值;
(2)数列{an}能否是等比数列?请说明理由;
(3)求证:当r=2时,数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量 ![]() =m
=m ![]() +n
+n ![]() (m,n为实数),则m+n的取值范围是( )
(m,n为实数),则m+n的取值范围是( ) 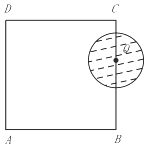
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com