
【题目】已知椭圆的一个顶点为A(0,-1),焦点在x轴上。若右焦点F到直线x-y+2![]() =0的距离为3。
=0的距离为3。
(1)求椭圆的方程;
(2)设直线y=kx+m(k≠0)与椭圆相交于不同的两点M、N。当|AM|=|AN|时,求m的取值范围。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据右焦点到直线x﹣y+![]() =0的距离为3,利用点到直线的距离公式求出c,再由椭圆的一个顶点为A(0,﹣1),求出b,从而得到椭圆方程.(2)设A为弦MN的中点,由
=0的距离为3,利用点到直线的距离公式求出c,再由椭圆的一个顶点为A(0,﹣1),求出b,从而得到椭圆方程.(2)设A为弦MN的中点,由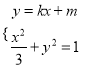 ,得(3k2+1)x2+6kmx+3(m2﹣1)=0.利用根的判别式和韦达定理,结合题设能求出m的取值范围.
,得(3k2+1)x2+6kmx+3(m2﹣1)=0.利用根的判别式和韦达定理,结合题设能求出m的取值范围.
解析:
(1) 设右焦点F(c,0),(c>0),则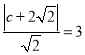 ,∴
,∴![]() .∵椭圆的一个顶点为A(0,﹣1),∴b=1,a2=3,∴椭圆方程是
.∵椭圆的一个顶点为A(0,﹣1),∴b=1,a2=3,∴椭圆方程是![]() .
.
(2)设P为弦MN的中点,由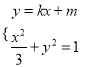 得(3k2+1)x2+6kmx+3(m2﹣1)=0.
得(3k2+1)x2+6kmx+3(m2﹣1)=0.
由△>0,得m2<3k2+1 ①,
∴xP=![]() ,
,
从而yP=kxp+m=![]() .
.
∴kBP=![]() .
.
由MN⊥AP,得![]() =﹣
=﹣![]() ,
,
即2m=3k2+1②.
将②代入①,得2m>m2,
解得0<m<2.由②得k2=![]() >0.
>0.
解得m>![]() .故所求m的取值范围为(
.故所求m的取值范围为(![]() ,2).
,2).


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为![]() ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省新乡市2017届高三上学期第一次调研】设![]() 为坐标原点,已知椭圆
为坐标原点,已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的准线方程为
的准线方程为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)设过定点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 在以
在以![]() 为直径的圆的外部,求直
为直径的圆的外部,求直
线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,
, ![]() 且
且![]() ,则
,则![]() 的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为
,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为 ![]()
(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M, ![]() =λ(
=λ( ![]() ),若点N在圆O上,求正实数λ的取值范围.
),若点N在圆O上,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民中学为了了解该校高一年级学生的数学成绩,从高一年级期中考试成绩中抽出100名学生的成绩,由成绩得到如下的频率分布直方图.
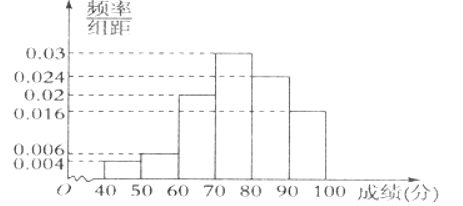
根据以上频率分布直方图,回答下列问题:
(1)求这100名学生成绩的及格率;(大于等于60分为及格)
(2)试比较这100名学生的平均成绩和中位数的大小.(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com