
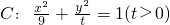 的左顶点,直线l:x=my+1(m∈R)与椭圆C相交于E,F两点,与x轴相交于点B.且当m=0时,△AEF的面积为
的左顶点,直线l:x=my+1(m∈R)与椭圆C相交于E,F两点,与x轴相交于点B.且当m=0时,△AEF的面积为 .
. 解得
解得 ,所以
,所以 .
. ,解得t=2.
,解得t=2.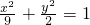 .
. 得(2m2+9)y2+4my-16=0,显然m∈R.
得(2m2+9)y2+4my-16=0,显然m∈R. ,x1=my1+1,x2=my2+1.
,x1=my1+1,x2=my2+1. ,
, 解得
解得 ,同理得
,同理得 .
. ,
, =
= =
=
 =
= =0.
=0. ,所以以MN为直径的圆过点B.
,所以以MN为直径的圆过点B. 得到关于t的方程,解出即可.
得到关于t的方程,解出即可. 消x得到关于y的一元二次方程,设E(x1,y1),F(x2,y2),由韦达定理可用m表示y1,y2,根据已知条件可求出M,N坐标,判断以MN为直径的圆是否经过点B,只需判断是否有
消x得到关于y的一元二次方程,设E(x1,y1),F(x2,y2),由韦达定理可用m表示y1,y2,根据已知条件可求出M,N坐标,判断以MN为直径的圆是否经过点B,只需判断是否有 ,进而转化为是否有
,进而转化为是否有 ,通过计算即可验证.
,通过计算即可验证.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| ||
|
|
| ||
|
|
| F1F2 |
| PQ |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 4 |
| 3 |
| 4 |
| 3 |
| ||
|
|
| ||
|
|
| F1F2 |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
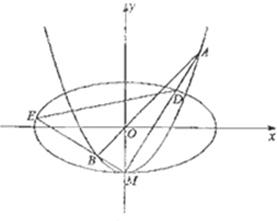 已知椭圆C1:
已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| TP |
| NP |
| S1 |
| S2 |
| 27 |
| 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 9 |
| y2 |
| t |
| 16 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com