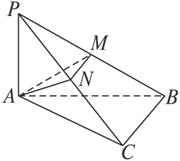
如图2-3-8,在斜边为AB的Rt△ABC中,过点A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.图2-3-8(1)求证:BC⊥平面PAC.(2)求证:PB⊥平面AMN. 题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：高中数学 来源： 题型：阅读理解

杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图是一个11阶杨辉三角：
（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为

2

3

，求n的值；
（3）求n阶（包括0阶）杨辉三角的所有数的和；
（4）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m、k（m，k∈N×）的数学公式表示上述结论，并给予证明．

第0行												1	…	…	…	…	…	…	…	…	…	…	…	…	第1斜列
第1行											1		1	…	…	…	…	…	…	…	…	…	…	…	第2斜列
第2行										1		2		1	…	…	…	…	…	…	…	…	…	…	第3斜列
第3行									1		3		3		1	…	…	…	…	…	…	…	…	…	第4斜列
第4行								1		4		6		4		1	…	…	…	…	…	…	…	…	第5斜列
第5行							1		5		10		10		5		1	…	…	…	…	…	…	…	第6斜列
第6行						1		6		15		20		15		6		1	…	…	…	…	…	…	第7斜列
第7行					1		7		21		35		35		21		7		1	…	…	…	…	…	第8斜列
第8行				1		8		28		56		70		56		28		8		1	…	…	…	…	第9斜列
第9行			1		9		36		84		126		126		84		36		9		1	…	…	…	第10斜列
第10行		1		10		45		120		210		252		210		120		45		10		1	…	…	第11斜列
第11行	1		11		55		165		330		462		462		330		165		55		11		1	…	第12斜列
										11阶杨辉三角

查看答案和解析>>

科目：高中数学 来源：2010-2011学年上海市浦东新区高三第一学期质量抽测数学理卷 题型：解答题

（本小题满分14分，第1小题满分6分，第2小题满分8分）

野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架（如图3）进行野炊训练. 已知，、两点间距离为.

（1）求斜杆与地面所成角的大小（用反三角函数值表示）；

（2）将炊事锅看作一个点，用吊绳将炊事锅吊起烧水（锅的大小忽略不计），若使炊事锅到地面及各条斜杆的距离都不小于30，试问吊绳长的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

（本小题满分14分，第1小题满分6分，第2小题满分8分）

野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架（如图3）进行野炊训练，将炊事锅看作一个点，用吊绳将炊事锅吊起烧水（锅的大小忽略不计）. 已知，、两点间距离为.

（1）设的延长线与地面的交点为，求的值；

（2）若使炊事锅到各条斜杆的距离都等于30，试求吊绳的长.

查看答案和解析>>

科目：高中数学 来源： 题型：

（本小题满分14分，第1小题满分6分，第2小题满分8分）

野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架（如图3）进行野炊训练. 已知，、两点间距离为.

（1）求斜杆与地面所成角的大小（用反三角函数值表示）；

（2）将炊事锅看作一个点，用吊绳将炊事锅吊起烧水（锅的大小忽略不计），若使炊事锅到地面及各条斜杆的距离都不小于30，试问吊绳长的取值范围.

查看答案和解析>>

科目：高中数学 来源：2011-2012学年福建省泉州市晋江市季延中学高二（下）期末数学试卷（理科）（解析版） 题型：解答题

杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图是一个11阶杨辉三角：
（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为

，求n的值；
（3）求n阶（包括0阶）杨辉三角的所有数的和；
（4）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m、k（m，k∈N×）的数学公式表示上述结论，并给予证明．

第0行												1	…	…	…	…	…	…	…	…	…	…	…	…	第1斜列
第1行											1		1	…	…	…	…	…	…	…	…	…	…	…	第2斜列
第2行										1		2		1	…	…	…	…	…	…	…	…	…	…	第3斜列
第3行									1		3		3		1	…	…	…	…	…	…	…	…	…	第4斜列
第4行								1		4		6		4		1	…	…	…	…	…	…	…	…	第5斜列
第5行							1		5		10		10		5		1	…	…	…	…	…	…	…	第6斜列
第6行						1		6		15		20		15		6		1	…	…	…	…	…	…	第7斜列
第7行					1		7		21		35		35		21		7		1	…	…	…	…	…	第8斜列
第8行				1		8		28		56		70		56		28		8		1	…	…	…	…	第9斜列
第9行			1		9		36		84		126		126		84		36		9		1	…	…	…	第10斜列
第10行		1		10		45		120		210		252		210		120		45		10		1	…	…	第11斜列
第11行	1		11		55		165		330		462		462		330		165		55		11		1	…	第12斜列
										11阶杨辉三角

查看答案和解析>>

练习册

高中

初中

小学