
| A. | m+n | B. | -(m+n) | C. | n-m | D. | m-n |
分析 利用二阶行列式展开法则进行求解.
解答 解:∵$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|=m,|\begin{array}{l}{{a}_{13}}&{{a}_{11}}\\{{a}_{23}}&{{a}_{21}}\end{array}|$=n,
∴m=a11a22-a21a12,
n=a13a21-a23a11,
∴$|\begin{array}{l}{{a}_{11}}&{{a}_{12}+{a}_{13}}\\{{a}_{21}}&{{a}_{22}+{a}_{23}}\end{array}|$=a11(a22+a23)-a21(a12+a13)
=a11a22-a21a12-(a21a13-a23a11)
=m-n.
故选:D.
点评 本题考查二阶行列式的计算,是基础题,解题时要注意二阶行列式展开法则的合理运用.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
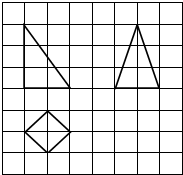 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com