
分析 (I)当t=1时,求出函数f(x),利用导数的几何意义求出x=0处的切线的斜率,利用点斜式求出切线方程;
(II)根据f'(x)=0,解得x=-t或x=$\frac{t}{2}$,讨论t的正负,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0求出单调区间即可;
(III)根据函数的单调性分两种情况讨论,当$\frac{t}{2}$≥1与当0<$\frac{t}{2}$<1时,研究函数的单调性,然后根据区间端点的符号进行判定对任意t∈(0,2),f(x)在区间(0,1)内均存在零点从而得到结论.
解答 解:(I)当t=1时,f(x)=2x3+$\frac{3}{2}$x2-3x,f(0)=0,
f'(x)=6x2+3x-3,f'(0)=-3,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-3x;
(II)解:f'(x)=6x2+3tx-3t2,
f'(x)=0,解得x=-t或x=$\frac{t}{2}$,
∵t≠0,以下分两种情况讨论:
(1)若t<0,则$\frac{t}{2}$<-t,∴f(x)的单调增区间是(-∞,$\frac{t}{2}$),(-t,+∞);
f(x)的单调减区间是($\frac{t}{2}$,-t);
(2)若t>0,则$\frac{t}{2}$>-t,∴f(x)的单调增区间是(-∞,-t),($\frac{t}{2}$,+∞);
f(x)的单调减区间是(-t,$\frac{t}{2}$);
(III)证明:由(II)可知,当t>0时,f(x)在(0,$\frac{t}{2}$)内单调递减,
在($\frac{t}{2}$,+∞)内单调递增,以下分两种情况讨论:
(1)当$\frac{t}{2}$≥1,即t≥2时,f(x)在(0,1)内单调递减.
f(0)=$\frac{1}{2}$(t-1)>0,f(1)=-3t2+2t+$\frac{3}{2}$<0,
所以对于任意t∈[2,+∞),f(x)在区间(0,1)内均存在零点.
(2)当0<$\frac{t}{2}$<1,即0<t<2时,f(x)在(0,$\frac{t}{2}$)内单调递减,
在($\frac{t}{2}$,1)内单调递增;
若t∈(0,1],f($\frac{t}{2}$)=-$\frac{7}{8}$t3+$\frac{1}{2}$(t-1)≤-$\frac{7}{8}$t3<0,
f(1)=-3t2+2t+$\frac{3}{2}$≥-t+$\frac{3}{2}$>0,
所以f(x)在($\frac{t}{2}$,1)内存在零点.
若t∈(1,2),f($\frac{t}{2}$)=-$\frac{7}{8}$t3+$\frac{1}{2}$(t-1)<-$\frac{7}{8}$t3+1<0,f(0)=$\frac{1}{2}$(t-1)>0,
∴f(x)在(0,$\frac{t}{2}$)内存在零点.
所以,对任意t∈(0,2),f(x)在区间(0,1)内均存在零点.
综上,对于任意t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
点评 本题主要考查了导数的几何意义,利用导数研究函数的单调性、曲线的切线方程、函数零点、解不等式等基础知识,考查了计算能力和分类讨论的思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
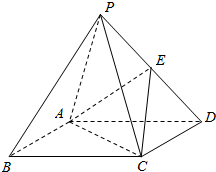 如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.
如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com