
分析 由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,如图所示,将P-ABC视为正方体的一部分,球的半径R=3$\sqrt{2}$,OP=2$\sqrt{2}$,即可求出该三棱锥外接球球心O到平面ABC的距离.
解答 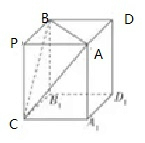 解:由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,
解:由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,
如图所示,将P-ABC视为正方体的一部分,球的半径R=3$\sqrt{2}$,
OP=2$\sqrt{2}$,
所以该三棱锥外接球球心O到平面ABC的距离为3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查球内接多面体的性质的应用,考查了计算能力和数形结合思想,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:选择题
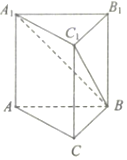 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 011 | B. | -2 012 | C. | -2 010 | D. | -2 013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com