
| X1 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 0.03 | 0.09 | 0.20 | 0.31 | 0.27 | 0.10 |
| X2 | 5 | 6 | 7 | 8 | 9 |
| P | 0.01 | 0.05 | 0.20 | 0.41 | 0.33 |
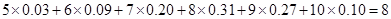 ,EX2=
,EX2=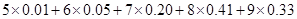 =8
=8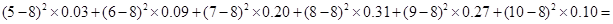 1.50 DX2=
1.50 DX2=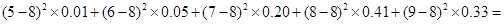 0.8
0.8

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源:不详 题型:解答题
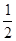 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
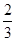 ,乙获胜的概率为
,乙获胜的概率为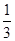 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
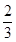 ,被乙小组攻克的概率为
,被乙小组攻克的概率为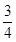 ,
,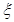 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求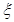 的分布列及数学期望
的分布列及数学期望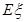 ;
;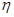 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数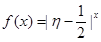 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
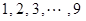 班参加高考体检,
班参加高考体检,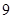 个班中,任选
个班中,任选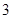 个班先参加视力检查. (I)求这
个班先参加视力检查. (I)求这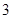 个班中恰有
个班中恰有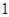 个班班级序号是偶数的概率;
个班班级序号是偶数的概率;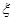 为这
为这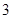 个班中两班序号相邻的组数(例如:若选出的班为
个班中两班序号相邻的组数(例如:若选出的班为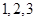 班,则有两组相邻的,
班,则有两组相邻的,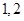 班和
班和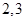 班,此时
班,此时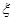 的值是
的值是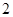 ).求随机变量
).求随机变量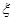 的分布列及其数学期望
的分布列及其数学期望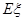 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
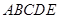 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.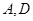 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;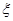 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量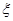 的分布列及其数学期望.
的分布列及其数学期望.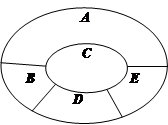
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com