练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    现有5名男司机，4名女司机，需选派5人运货到吴忠．
    (1)如果派3名男司机、2名女司机，共多少种不同的选派方法？
    (2)至少有两名男司机，共多少种不同的选派方法？

    (1)；(2) 121．

    解析试题分析:解排列组合的应用题一定要仔细审题，判断是排列问题还是组合问题，要按元素的性质进行分类，按事件发生的过程进行分步， (1)先从5名男司机中选3名，再从4名女司机中选2名，可用分步乘法原理；(2)至少两名男司机，先分类可分为2男3女，3男2女，4男1女，5男，再在每一类中应用分步．
    解：（1）利用分步乘法原理：,
    （2）利用分类加法与分步乘法原理：
    ．
    考点：分步乘法原理，分类加法原理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    有9本不同的课外书，分给甲、乙、丙三名同学，求在下列条件下，各有多少种分法？
    (1)甲得4本，乙得3本，丙得2本；
    (2)一人得4本，一人得3本，一人得2本；
    (3)甲、乙、丙各得3本．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知在的展开式中，第5项的系数与第3项的系数之比是56：3．
    （1）求展开式中的所有有理项；
    （2）求展开式中系数绝对值最大的项．
    （3）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7名师生站成一排照相留念，其中老师1人，男生4人，女生2人，在下列情况下，各有不同站法多少种?（用数字作答）
    （1）两名女生必须相邻而站；
    （2）4名男生互不相邻.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如果的展开式中，第四项和第七项的二项式系数相等，求：
    (1)展开式的中间项；
    (2)展开式中所有的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设，且，其中当为偶数时，；当为奇数时，．
    （1）证明：当，时，；
    （2）记，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10双互不相同的鞋子混装在一个袋子中，从中任意取4只，4只鞋子中有两只成双，另两只不成双的取法数为_        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    将并排的有不同编号的5个房间安排给5个工作人员临时休息，假定每个人可以选择任一房间，且选择各个房间是等可能的，求恰有2个房间无人选择且这2个房间不相邻的安排方式的种数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).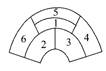

    查看答案和解析>>

    同步练习册答案